বাংলায় মেশিন লার্নিং
অন্যান্য কোর্স
Search…
⌃K
Links

লিনিয়ার রিগ্রেশন পর্ব-২ ও গ্রেডিয়েন্ট ডিসেন্ট

লিনিয়ার রিগ্রেশন : দ্বিতীয় পর্ব

আমরা গত পর্বে লিনিয়ার রিগ্রেশনের বেসিক জানার পাশাপাশি কস্ট ফাংশন ক্যালকুলেশন সম্পর্কে কিছুটা জেনেছিলাম। আজকে আমরা নিচের বিষয়গুলো সম্পর্কে জানার চেষ্টা করব।

আজকের আলোচনার বিষয়বস্তু

  • কস্ট ফাংশন ইনটুইশন - ২
    • ​
      J(θ)J(\theta)
       এর গ্রাফ
  • গ্রেডিয়েন্ট ডিসেন্ট (Gradient Descent) অপ্টিমাইজেশন

কস্ট ফাংশন ইনটুইশন

এতক্ষণে লিনিয়ার মডেল সম্পর্কে ভালই ধারণা হয়েছে আশা করি, সেটা যদি হয়ে থাকে আমরা আরেকবার ঘুরে আসি কস্ট ফাংশনের কাছ থেকে।

কস্ট ফাংশনের গ্রাফ দিয়ে লাভ কী?

আমাদের কাজ ছিল কস্ট মিনিমাইজ করা। সকল ইঞ্জিনিয়ারিংয়ের মূল লক্ষ্য তাই। যত কম রিসোর্স ব্যবহার করে যত ভাল ফলাফল পাওয়া যায়। তেমনি মেশিন লার্নিংয়ের জন্য আমাদের মূল লক্ষ্য থাকবে কতটা নির্ভুল প্রেডিকশন করা যায়।
আমরা যদি কতগুলো মডেলের কস্ট ফাংশন এর রেজাল্ট স্ক্যাটার প্লট করি তাহলে আমরা গ্রাফ থেকে সহজেই ট্র্যাক করতে পারব সবচেয়ে কম এরর কোন প্যারামিটারের জন্য।
সবকিছু বাদ দিয়ে নতুন করে একটা জিনিস দেখা যাক, নিচের ডেটাসেট এর কথা চিন্তা করা করি,
আয় (X)
ব্যয় (Y)
10
5
100
50
1000
500
গ্রাফ
এই ডেটাসেটের গ্রাফ এইরকম,
graph
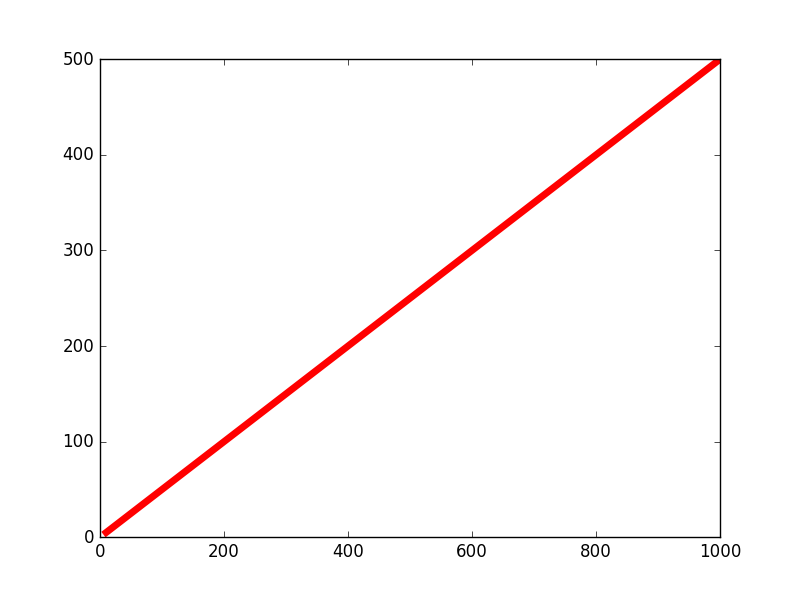
এটা প্রেডিক্ট করার জন্য আমরা এই মডেল ব্যবহার করব :
h0(θ)=θ×Xh_{0}(\theta) = \theta \times X
​
বিভিন্ন
θ\theta
 এর মানের জন্য আমরা
J(θ)J(\theta)
 প্লট করব। মানে প্রতি প্রেডিকশনে কস্ট ক্যালকুলেট করব। তারপর দেখব
θ\theta
 এর কোন মানের জন্য
J(θ)J(\theta)
 এর মান সর্বনিম্ন আসে।

​
h0(θ)=θ×Xh_{0}(\theta) = \theta \times X
 সাপেক্ষে
J(θ)J(\theta)
​

ধরি
θ=0.1\theta = 0.1
​

তাহলে প্লট আসবে এরকম,
hypo1
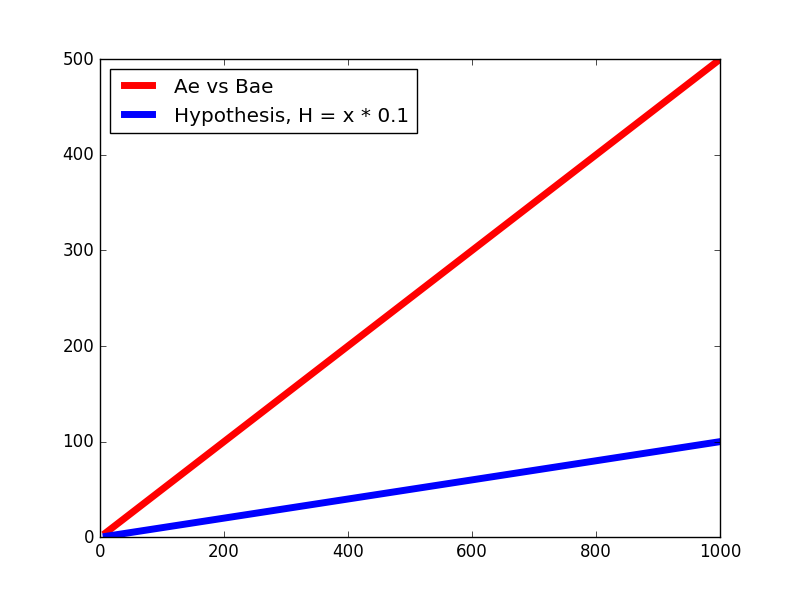
কস্ট ক্যালকুলেশন:
J(0.1)=12×3×42+402+4002=26936.0J(0.1) = \frac{1}{2 \times 3} \times { 4^{2} + 40^{2} + 400^{2} } = 26936.0
​

আবার ধরি
θ=0.2\theta = 0.2
​

তাহলে প্লট,
hypo2
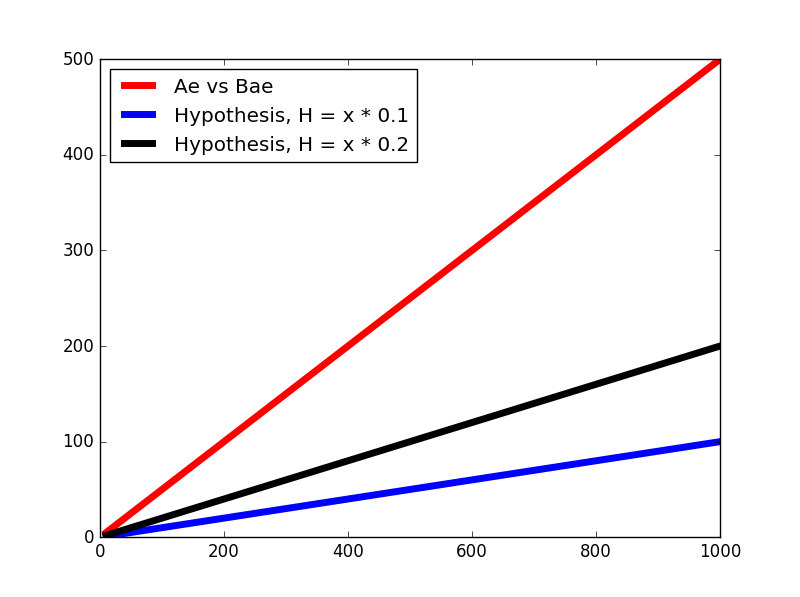
কস্ট ক্যালকুলেশন:
J(0.2)=12×3×32+302+3002=15151.5J(0.2) = \frac{1}{2 \times 3} \times { 3^{2} + 30^{2} + 300^{2} } = 15151.5
​

আবার ধরি
θ=0.3\theta = 0.3
​

তাহলে প্লট,
hypo3
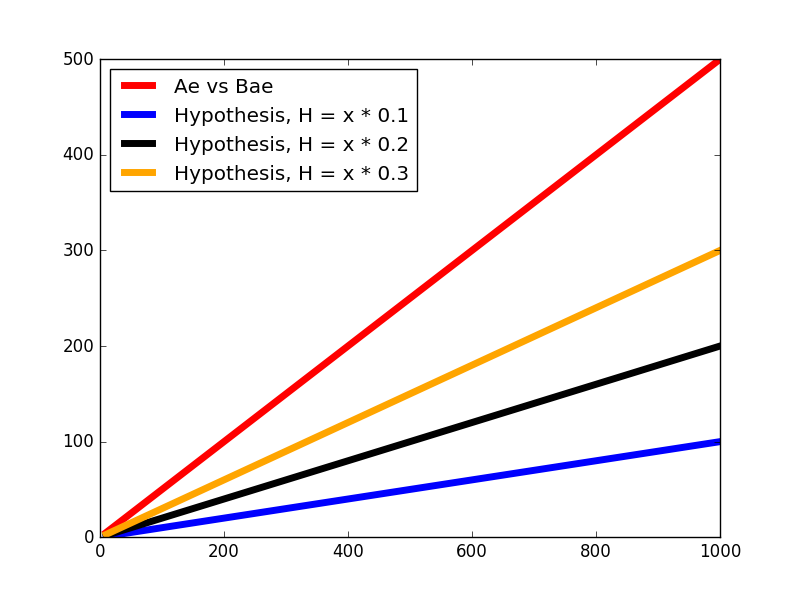
কস্ট ক্যালকুলেশন:
J(0.3)=12×3×22+202+2002=6734.0J(0.3) = \frac{1}{2 \times 3} \times { 2^{2} + 20^{2} + 200^{2} } = 6734.0
​

আবারও ধরি
θ=0.4\theta = 0.4
​

hypo4
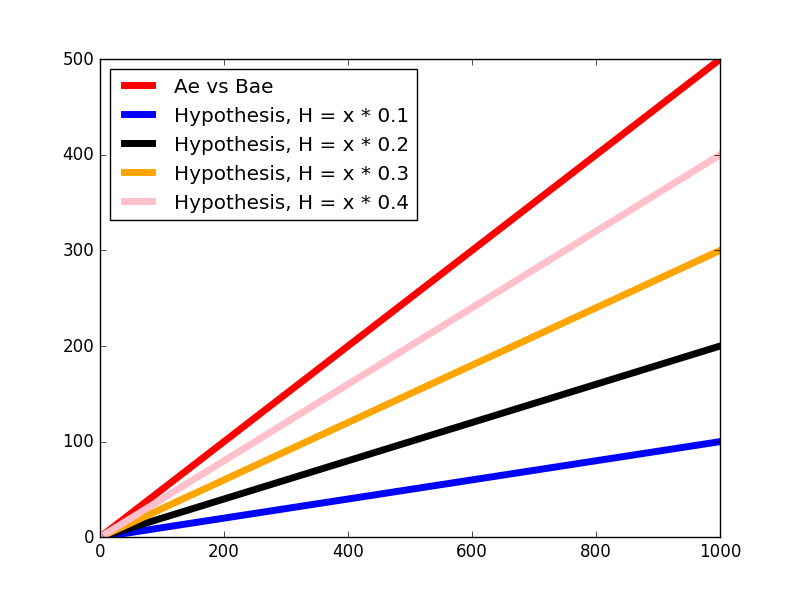
কস্ট ক্যালকুলেশন:
J(0.4)=12×3×12+102+1002=1683.5J(0.4) = \frac{1}{2 \times 3} \times { 1^{2} + 10^{2} + 100^{2} } = 1683.5
​

​
θ=0.5\theta = 0.5
​

hypo5
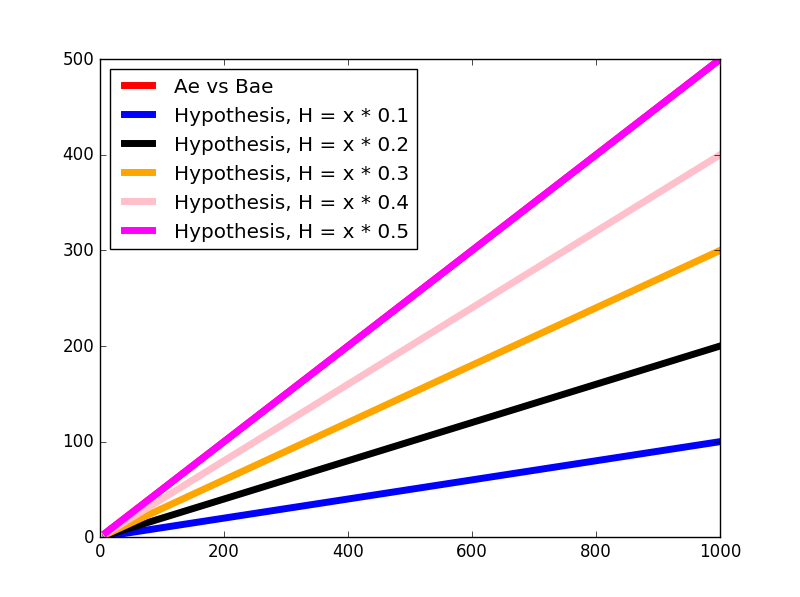
কস্ট ক্যালকুলেশন:
J(0.5)=12×3×02+02+02=0J(0.5) = \frac{1}{2 \times 3} \times { 0^{2} + 0^{2} + 0^{2} } = 0
​

থিটা এর মান আরও বাড়ালে,
θ=0.6\theta = 0.6
​

hypo6
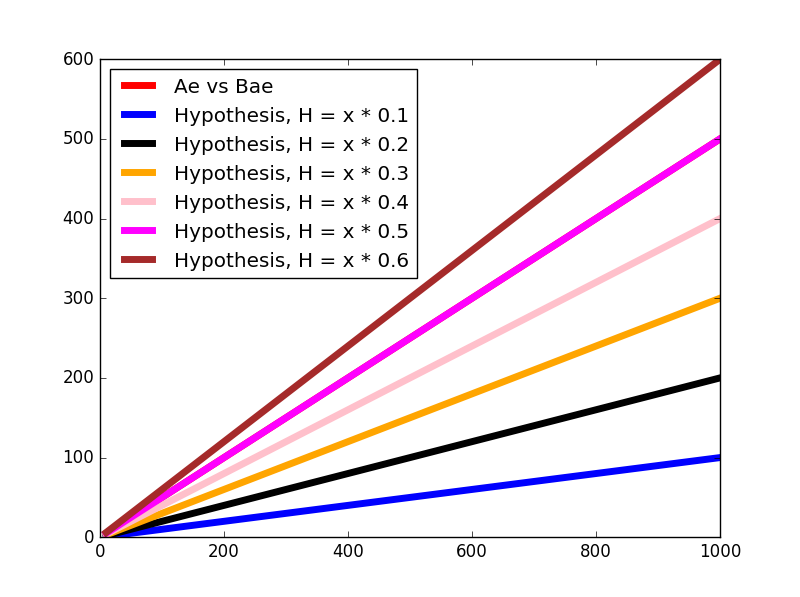
কস্ট ক্যালকুলেশন:
J(0.6)=12×3×(−1)2+(−10)2+(−100)2=1683.5J(0.6) = \frac{1}{2 \times 3} \times { (-1)^{2} + (-10)^{2} + (-100)^{2} } = 1683.5
​

আরও বাড়িয়ে
θ=0.7\theta = 0.7
​

hypo7
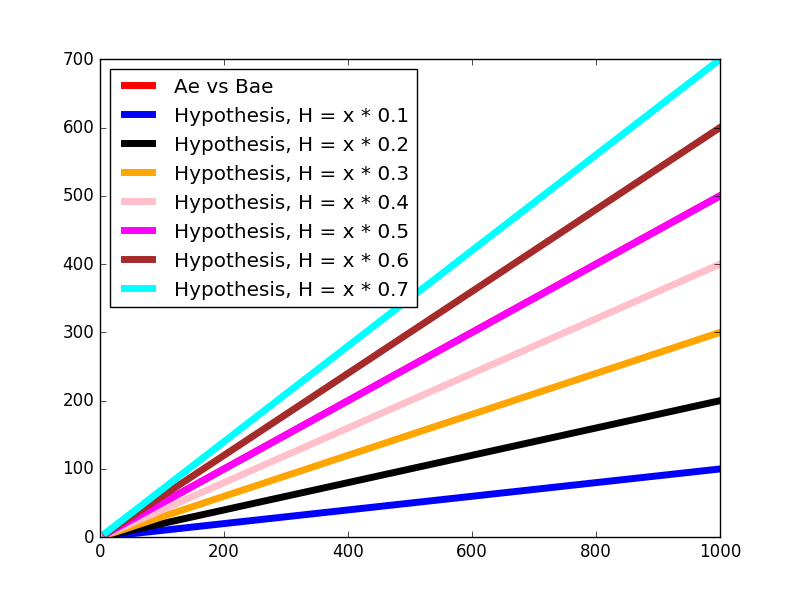
কস্ট ক্যালকুলেশন:
J(0.7)=12×3×(−2)2+(−20)2+(−200)2=6734.0J(0.7) = \frac{1}{2 \times 3} \times { (-2)^{2} + (-20)^{2} + (-200)^{2} } = 6734.0
​
থাক আর বাড়ালাম না, এখন আমরা প্রতি থিটার মানের জন্য যতগুলো
J(θ)J(\theta)
 এর মান পেয়েছি সেগুলোর স্ক্যাটার প্লট তৈরি করি,

কস্ট ফাংশন গ্রাফ

costfunc
J = [26936.0, 15151.5, 6734.0, 1683.5, 0, 1683.5, 6734.0]
theta = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7]
colors = ['blue', 'black', 'orange', 'pink', 'magenta', 'brown', 'aqua']
​
for i in range(len(J)):
lbl = 'Hypothesis H = %0.1f * x' % theta[i]
plt.scatter(x[i], J[i], linewidth=5, color=colors[i], label=lbl)
​
plt.legend(loc='best')
plt.title('Cost Function Graph')
plt.xlabel('Theta')
plt.ylabel('J (theta)')
plt.show()
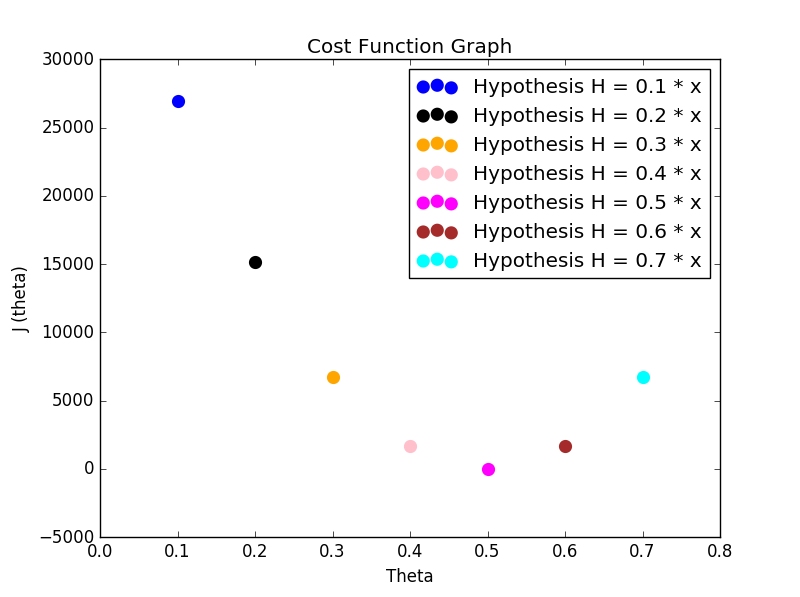
গ্রাফ থেকে কী বুঝলাম?
θ=0.5\theta = 0.5
 এর জন্য কস্ট সবেচেয়ে কম। মানে প্রেডিকশন সবেচেয়ে বেটার যখন থিটার মান
0.50.5
। এভাবে প্রতিটা মডেলের কস্ট ফাংশন থেকে আমরা ধারণা করতে পারি মডেলের পার্ফর্মেন্স কতটা ভাল।

যদি আমাদের মডেল
J(θ0,θ1)=θ0+θ1×xJ(\theta_{0}, \theta_{1}) = \theta_{0} + \theta_{1} \times x
 হত

তাহলে সেটার প্লট হতে পারত এরকম,
contourplot
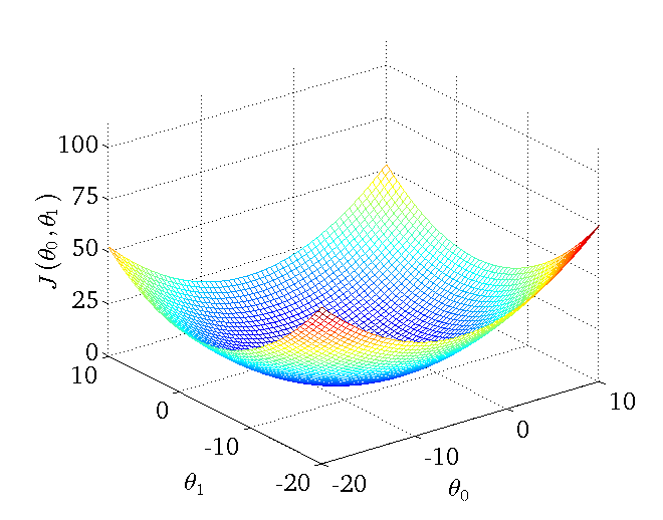
আমরা অবশেষে কস্ট ফাংশন সম্পর্কে অনেক কিছু জানতে পারলাম। এখন আমরা দেখব Cost Function Minimization Using Gradient Descent।

Gradient Descent অ্যালগরিদম

ক্যালকুলাস মনে আছে? ডিফারেনসিয়েশন? সেটাই আমাদের এখন কিছুটা কাজে আসবে। যদি মনে না থাকে তাহলে আগে একটু ডিফারেনসিয়েশন দেখা যাক।

Differentiation : Method for Calculating Slope at a specific point of a function

কোন বিন্দুতে কোন ফাংশনের ডেরিভেটিভ মানে হল সেই বিন্দুতে ঐ ফাংশনের স্পর্শকের ঢাল। ধরি,
y=f(x)y = f(x)
 যেকোন একটি ফাংশন, এখন আমরা তার
(x1,y1)(x_{1}, y_{1})
 বিন্দুতে যে স্পর্শক, তার ঢাল (
XX
 অক্ষের সাথে রেখাটি কত ডিগ্রি কোণ উৎপন্ন করে) জানতে চাই। তাহলে আমরা
f(x)f(x)
 কে স্বাধীন চলক
xx
 এর সাপেক্ষে ডিফারেনসিয়েট করব। ডিফারেনসিয়েট অপারেটর টা লেখে এইভাবে
dydx\frac{dy}{dx}
 বা
df(x)dx\frac{df(x)}{dx}
 ।
নিচের ছবিটা দেখা যাক,
diff

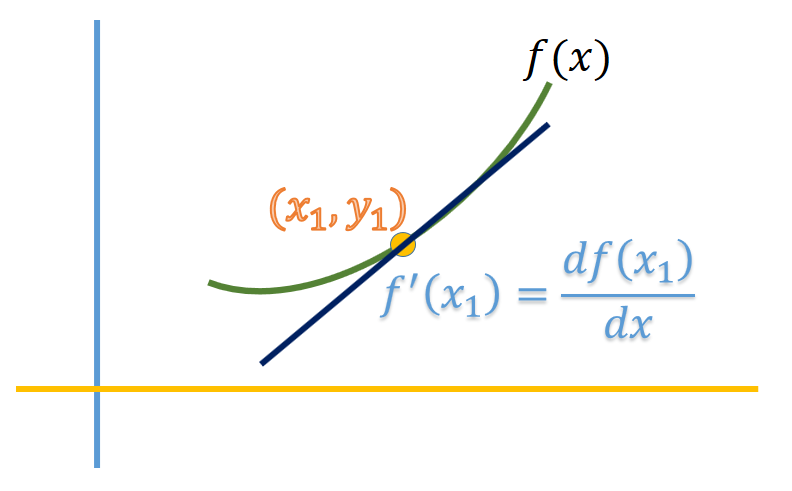
Slope বা ঢাল

slp
ঢালের সূত্র হচ্ছে ,
m=ΔyΔxm = \frac{\Delta y}{\Delta x}
​
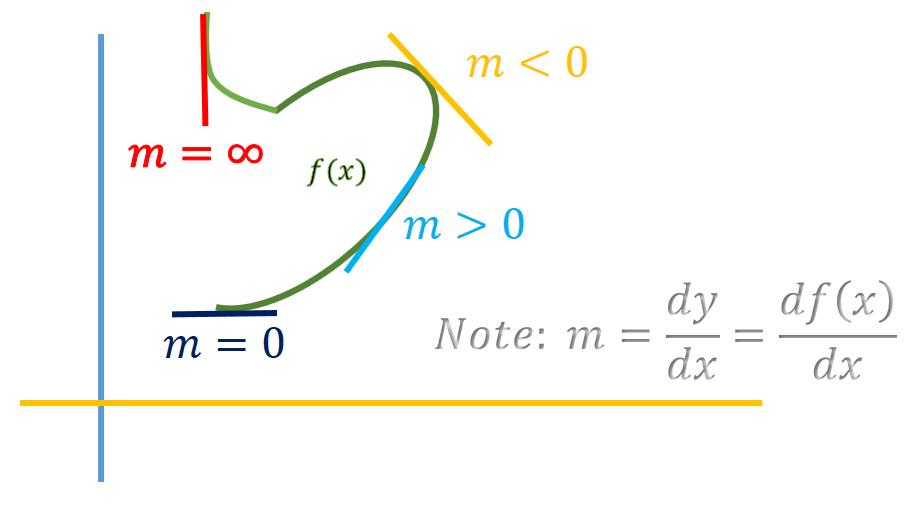
ঢালের মান চার ধরণের, নন-জিরো পজিটিভ, নেগেটিভ, জিরো এবং অসংজ্ঞায়িত। এই মানের ভিত্তিতে আমরা ঢালকে ক্লাসিফাই করতে পারি।

এই ঢাল চার ভাগ করা যায়,

  • ধনাত্মক ঢাল (Positive Slope)
    • যে ঢাল
      XX
       অক্ষের সাথে সূক্ষ্মকোণ উৎপন্ন করে সেটাকে ধনাত্মক ঢাল বলে। ধনাত্মক ঢাল আসলে বলে তার দিকে গেলে
      yy
       এর মান বাড়বে।
  • ঋণাত্মক ঢাল (Negative Slope)
    • যে ঢাল
      XX
       অক্ষের সাথে স্থূলকোণ উৎপন্ন করে সেটাকে ঋণাত্মক ঢাল বলে। ঋণাত্মক ঢাল বলে তার দিকে গেলে
      yy
       এর মান কমবে।
  • শূন্য ঢাল (Zero Valued Slope)
    • যে ঢাল
      XX
       অক্ষের সাথে
      00
       ডিগ্রি কোণ উৎপন্ন করে সেটাকে শূন্য ঢাল বলে।
  • অসংজ্ঞায়িত ঢাল (Undefined Slope)
    • যে ঢাল
      XX
       অক্ষের সাথে
      9090
       ডিগ্রি উৎপন্ন করে সেটাকে ধনাত্মক ঢাল বলে।
একনজরে ঢালগুলো,
slopes

Partial Derivative

আমাদের মূলত কাজে লাগবে পার্শিয়াল ডেরিভেটিভ। একটা ফাংশন যে সব সময় একটা ভ্যারিয়েবলের উপর ডিপেন্ডেন্ট থাকবে সেটা সত্য নয়। যেমন:
z=f(x,y)=x2+xy+y2z = f(x, y) = x^{2} + xy + y^{2}
 এই ফাংশনটার কথাই চিন্তা করা যাক, এখানে
zz
 ভ্যারিয়েবলটি
x,yx, y
 দুইটার উপর নির্ভরশীল। তাই আমরা যদি
xx
 ও
yy
 দুইটার সাপেক্ষে
zz
 এর পরিবর্তন ট্র্যাক করতে চাই তাহলে একটা ডেরিভেটিভ দিয়ে হবে না।
​
z=x2+xy+y2z = x^{2} + xy + y^{2}
​
​
δzδx=2x+y\frac{\delta z}{\delta x} = 2x + y
 যখন
yy
 ধ্রুবক
​
δzδy=2y+x\frac{\delta z} {\delta y} = 2y + x
 যখন
xx
 ধ্রুবক
আমরা যদি
θ1\theta_{1}
 প্যারামিটার দিয়ে কস্ট ফাংশন ক্যালকুলেট করি তাহলে আমাদের সাধারণ ডেরিভেটিভ নিলেই হচ্ছে, কিন্তু যদি
θ0,θ1\theta_{0}, \theta_{1}
 দুই কিংবা তার বেশি প্যারামিটার বিশিষ্ট কস্ট ফাংশন নেই তাহলে আমাদের অবশ্যই পার্শিয়াল ডেরিভেটিভ নিতে হবে। আপাতত আমরা এক প্যারামিটার বিশিষ্ট কস্ট ফাংশন দিয়ে গ্রেডিয়েন্ট ডিসেন্ট বোঝার চেষ্টা করব।
প্রশ্ন আসতে পারে, এই ঢাল দিয়ে আমরা করব টা কী? আসলে ক্যালকুলাসের সামান্য(!) কনসেপ্ট দিয়ে আমরা বিলিওন বিলিওন সেকেন্ড বাঁচাতে পারি।
আমরা ডিফারেনসিয়েশন ও ঢালের কনসেপ্ট দিয়ে কস্ট মিনিমাইজ করার চেষ্টা করব। আর সেই চেষ্টার জন্য আমরা যে অ্যালগরিদম ব্যবহার করব সেটাই Gradient Descent।

গ্রেডিয়েন্ট ডিসেন্ট

অ্যালগরিদম

repeat until convergence {
​
θj:=θj−αδδθjJ(θj)\theta_{j} := \theta_{j} - \alpha \frac{\delta}{\delta \theta_{j}} J(\theta_{j})
​
}
ম্যাথমেটিক্যাল নোটেশন
মানে
ম্যাথ
প্রোগ্রামিং
x ও y সমান
x= y
x == y
y এর মান x এ অ্যাসাইন করা
x := y
x = y
x আপডেট উদাহরণ
x := x + 1
x = x + 1
  • তারমানে
    :=:=
     এইটা দিয়ে বোঝানো হচ্ছে
    θj\theta_{j}
     এর মান প্রতিবার আপডেট করতে হবে।
  • এখানে
    α\alpha
     হল লার্নিং রেট (Learning Rate)
    গ্রেডিয়েন্ট ডিসেন্ট ইনটুইশন
অ্যালগরিদম আসলে কী বলছে? আমরা আগেই জানি মেশিন লার্নিং মডেল ট্রেইনিং মানে হচ্ছে মডেলের ইন্টার্নাল প্যারামিটার গুলো এমন ভাবে সেট করা যাতে আমাদের প্রেডিকশন নির্ভুল হয়। আমরা কয়েকটা গ্রাফের মাধ্যমে বোঝার চেষ্টা করি আসলে গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদমের কাজটা কী।

ধরি আমাদের কস্ট ফাংশন
J(θ1)J(\theta_{1})
​

এইবার যেকোন একটা
θ1\theta_{1}
 এর মান ধরি, এবং সেই বিন্দুতে ডিফারেনসিয়েট করি। যদি ঢাল ধনাত্মক হয়, এর মানে ঐদিকে গেলে
J(θ1)J(\theta_{1})
 মান বাড়বে এবং উল্টা দিকে গেলে তার মান কমবে। নিচের ছবিটা দেখলেই বুঝা যাবে।
graddescent1
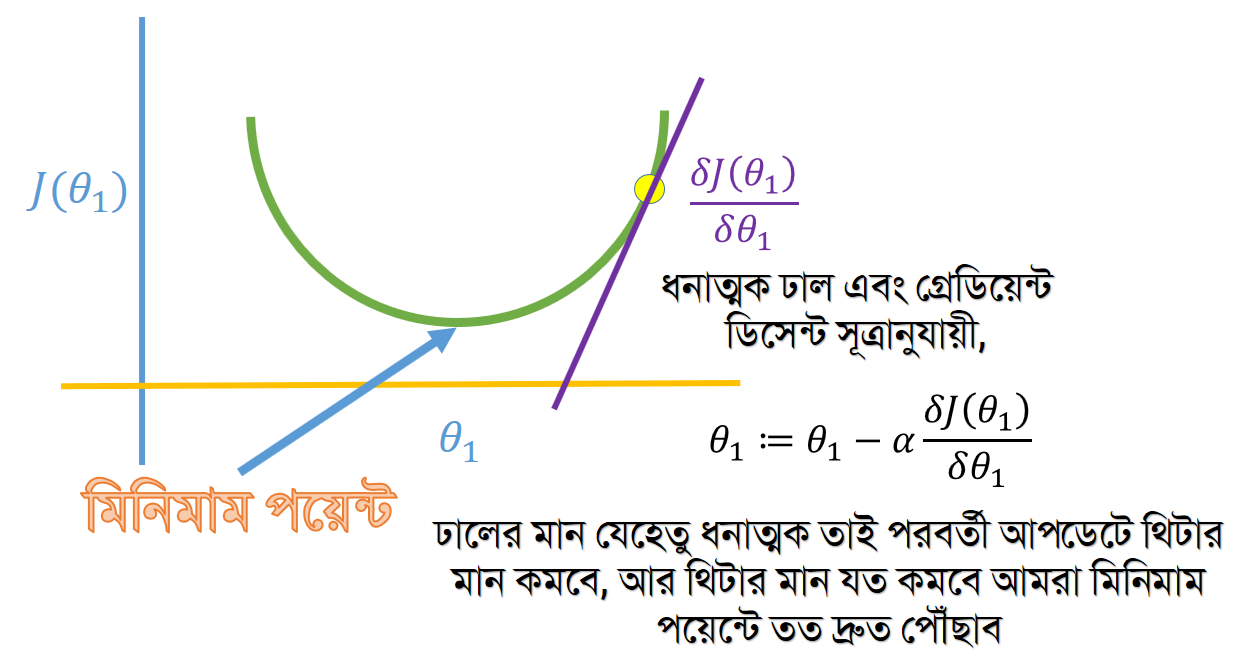
এইবার আমরা আরেকটা বিন্দু ধরি, যেটা কিনা লোকাল মিনিমাম এর বামে অবস্থান করে।
graddescent2
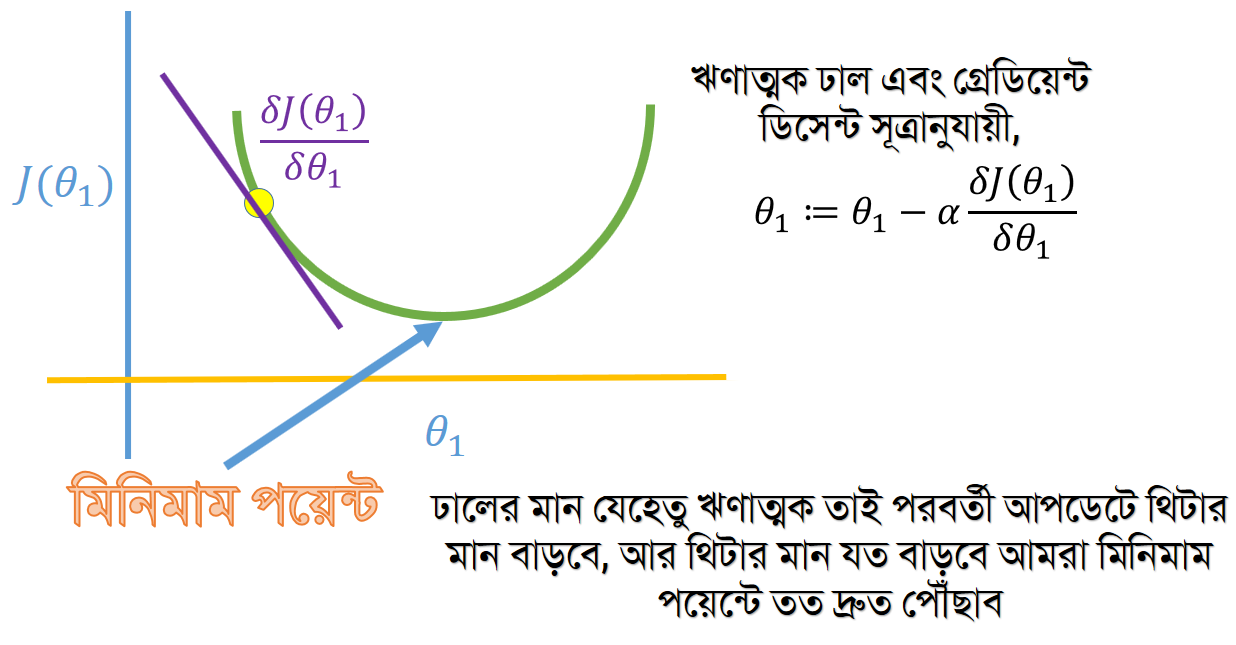
অর্থাৎ গ্রেডিয়েন্ট ডিসেন্ট সূত্রটি বলছে আমাদের কোন দিকে গেলে কস্ট ফাংশনটা মিনিমাইজ হবে। এটা হল যখন একটা প্যারামিটার। এইরকম শত শত প্যারামিটারের সময় ভিজুয়ালাইজ করাটা সুবিধাজনক নয় তবে সব ক্ষেত্রে কাজটা ঠিক এইভাবেই হয়ে থাকে।
এই আপডেট ততক্ষণ চলতে থাকে যতক্ষণ না মিনিমাম পয়েন্টে পৌঁছাবেন। মিনিমাম পয়েন্টে অ্যালগরিদমটি অটোমেটিক স্টপ হয়ে যাবে কারণ মিনিমাম পয়েন্টে
δJ(θ1)δθ1=0\frac{\delta J(\theta_{1})}{\delta \theta_{1}} = 0
 আর গ্রেডিয়েন্ট অংশ যদি
00
 হয় তাহলে আপডেটের কিছু থাকবে না।
এই পর্ব এই পর্যন্তই, পরবর্তী পর্বে আরেকদফা লিনিয়ার রিগ্রেশন, মাল্টি প্যারামিটারে গ্রেডিয়েন্ট ডিসেন্ট এবং ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট সম্পর্কে জানতে পারব।

সচরাচর জিজ্ঞাস্য প্রশ্ন

লার্নিং রেট কী?

লার্নিং রেট বা
α\alpha
 বলতে বুঝায় (ফিজিক্যাল মিনিং) কত দ্রুত কস্ট ফাংশন লোকাল মিনিমামে কনভার্জ করতে চান। লার্নিং রেট কমালে
θ1\theta_{1}
 এর মান মিনিমামে কনভার্জ করতে সময় (ইটারেশন) বেশি নিবে মানে অনেকবার আপডেট হতে হবে। লার্নিং বাড়ালে আপডেট কম হবে। এই আলফা হতে হবে যেকোন পজিটিভ সংখ্যা।

লার্নিং রেট বাড়ালে বা কমালে কী ইফেক্ট সৃষ্টি হতে পারে?

মনে করুন, আপনার চোখে পট্টি বেঁধে একটা উচুনিচু ভূমিতে ছেড়ে দেওয়া হল। এবং বলা হল, আপনার কাজ হবে সবচেয়ে নিচু জায়গাটা বের করা। এখন যদি আপনি বড় বড় স্টেপে হাঁটেন তাহলে মিনিমাম পয়েন্ট এড়িয়ে যেতে পারেন, আবার ছোট ছোট স্টেপে হাঁটলে নিচু জায়গা বের করতে অনেক সময় লাগবে। এই যে স্টেপ নিচ্ছেন সেটাকে আমরা লার্নিং রেটের অ্যানালজি বলতে পারি।
alphaeffect

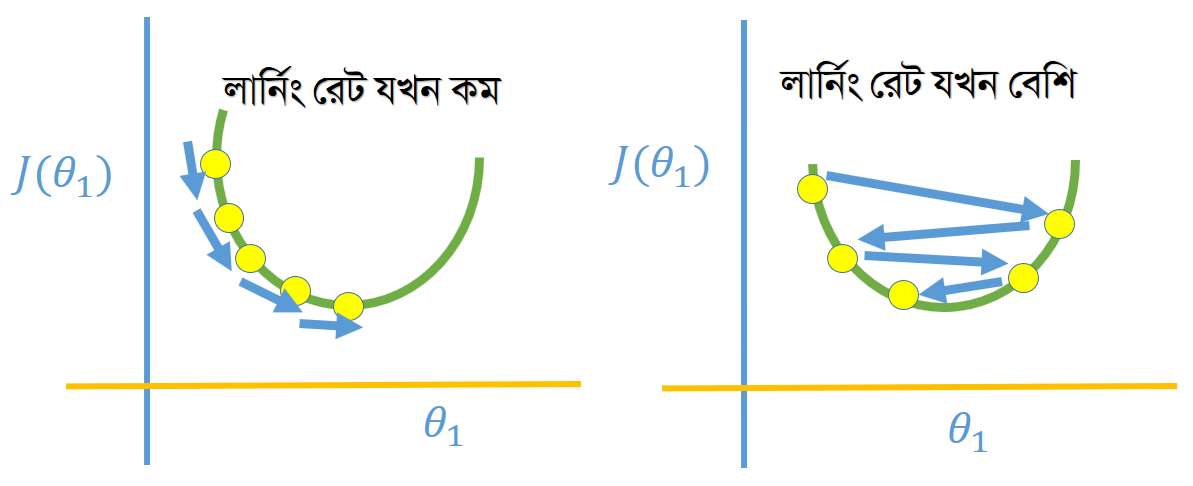
স্টেপের সাথে সাথে লার্নিং রেট বাড়ানো/কমানোর দরকার আছে কী?

না নেই, কারণ মিনিমাম লোকাল পয়েন্টের দিকে আগাতে থাকলে অটোমেটিক গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদমের আপডেট স্টেপ কমে যায়। তাই
α\alpha
 এর মান যদি ফিক্সড থাকে তাহলেও সেটা মিনিমাম পয়েন্টে কনভার্জ করবে।

​
θ1\theta_{1}
 এর মান বা সর্বোপরি প্যারামিটারগুলোর মান শুরুতে র‍্যান্ডম নেওয়ার উদ্দেশ্য কী?

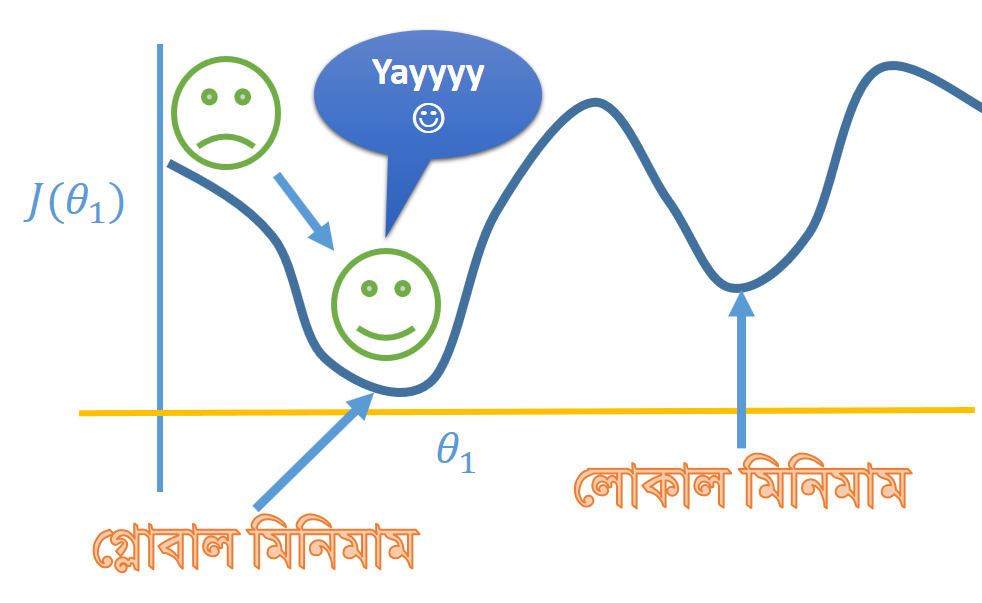
এই প্রশ্নের উত্তর অনেক বিশাল, র‍্যান্ডম পয়েন্টে প্যারামিটার ইনিশিয়ালাইজেশনের মূল সুবিধা হচ্ছে গ্লোবাল মিনিমাম বের করা। একই গ্রাফের লোকাল মিনিমাম বা গ্লোবাল মিনিমাম থাকতে পারে। লোকাল মিনিমাম বলতে সেই পয়েন্ট কে বোঝানো হয় যেটা সামগ্রিক গ্রাফের মধ্যে তুলনামূলক নিম্নবিন্দু। আর গ্লোবাল মিনিমাম হল পুরো গ্রাফের এমন একটা পয়েন্ট সেটাই সর্বনিম্ন বিন্দু।
আবার আমরা চোখে পট্টির উদাহরণে ব্যাক করি। ধরুন আপনাকে হেলিকপ্টারে করে এই পয়েন্টে ছেড়ে দিয়ে মিনিমাম পয়েন্ট বের করতে বলা হল। আপনি সোজা যেতে থাকলেন এবং লোকাল মিনিমাম বের করলেন। এখন যদি আপনাকে বার বার ঐ পয়েন্টেই ছাড়ি এবং আপনি সোজাই যেতে থাকেন আপনি প্রত্যেকটা বার লোকাল মিনিমাম পয়েন্ট পেয়ে লাফালাফি শুরু করে দেবেন।
localmin
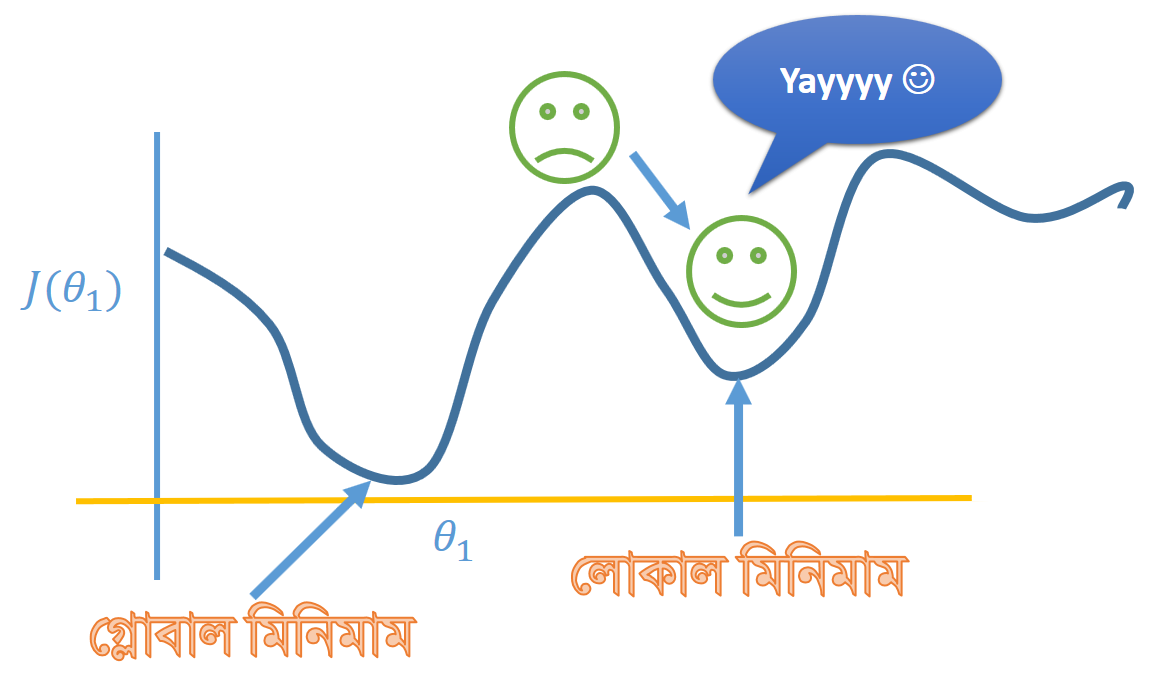
এবার আপনাকে র‍্যান্ডমলি হেলিকপ্টার থেকে এই বিন্দুতে ছাড়া হল এবং এইবার আপনি আসলেই গ্লোবাল পয়েন্টে যেতে পারবেন।
globalmin
Previous
লিনিয়ার রিগ্রেশন প্রাথমিক আলোচনা
Next
মাল্টিভ্যারিয়েবল লিনিয়ার রিগ্রেশন
Last modified 4yr ago