লিনিয়ার রিগ্রেশন প্রাথমিক আলোচনা

লিনিয়ার রিগ্রেশন : প্রাথমিক আলোচনা

এতদিনে আমরা মেশিন লার্নিংয়ের টার্গেট সম্পর্কে জানতে পারলাম। কিন্তু ম্যাথমেটিক্যাল মডেল কীভাবে কাজ করছে সেটা সম্পর্কে এখনো অজ্ঞ। এখনকার আলোচনা গুলোতে প্রেডিক্টিভ মডেল বিল্ডিংয়ের পাশাপাশি আমরা দেখব মডেলগুলো আসলে কীভাবে তৈরি হচ্ছে বা এর পিছনের লজিক টা আসলে কী।

আজকের আলোচনার বিষয়বস্তু

• লিনিয়ার রিগ্রেশন কী

• মডেল রিপ্রেজেন্টেশন (Model Representation)

• কস্ট ফাংশন (Cost Function)

• কস্ট ফাংশন ইনটুইশন (Cost Function Intuition)

শুরু করা যাক।

শুরু করার আগে আমরা বিখ্যাত বাড়ির দরদাম ডেটাসেট এর কথা চিন্তা করি। ‌ মনে করুন, আপনার বন্ধু রিয়েল এস্টেট বিজনেসম্যান এবং আপনি একজন ডেটা সায়েন্টিস্ট। আপনার বন্ধু আপনার সম্পর্কে জানতে পেরে ভাবল আপনাকে দিয়ে তার বিজনেসের কিছু কাজ করিয়ে নেবে বদলে আপনাকেও কিছু ৳ দেবে।

কাজটা হল, আপনার বন্ধুর কাছে একটা ডেটাসেট আছে, যেখানে বাড়ির আকার ও দরদাম দেওয়া আছে। আপনার যেটা করতে হবে, সেটা হল সেই ডেটাসেটে মেশিন লার্নিংয়ের বিশ্লেষণী ক্ষমতা অ্যাপ্লাই করে, যে বাড়ির আকার দেওয়া নেই সেই আকারের বাড়ির দাম প্রেডিক্ট করতে হবে।

আপনার বন্ধুর দেওয়া ডেটাসেট

বাড়ির সাইজ (একক - sq ft) (ধরি এটা X)	বাড়ির দাম (একক - ৳) (ধরি এটা, Y)
2104	399900
1600	329900
2400	369000
1416	232000
3000	539900
1985	299900
1534	314900
1427	198999
1380	212000
1494	242500
1940	239999
2000	347000
1890	329999
4478	699900
1268	259900
2300	449900
1320	299900
1236	199900
2609	499998
3031	599000
1767	252900
1888	255000
1604	242900
1962	259900
3890	573900
1100	249900
1458	464500
2526	469000
2200	475000
2637	299900
1839	349900
1000	169900
2040	314900
3137	579900
1811	285900
1437	249900
1239	229900
2132	345000
4215	549000
2162	287000
1664	368500
2238	329900
2567	314000
1200	299000
852	179900
1852	299900
1203	239500

এই সমস্যাটি আসলে রিগ্রেশন এর মধ্যে পড়ে, কীভাবে?

লিনিয়ার রিগ্রেশন

রিগ্রেশন:

রিগ্রেশন মানে Real-value আউটপুট প্রেডিক্ট করতে হবে। আরেক ধরণের প্রেডিকশন আমরা করে এসেছি (হ্যাঁ/না ভিত্তিক), সেটা হল ক্লাসিফিকেশন। তারমানে 10, 20, 30, বা 1236, 5.123 ইত্যদি ইত্যাদি প্রেডিক্ট করার মানেই হল আমি একটা রিগ্রেশন প্রবলেমে হাত দিয়েছি।

লিনিয়ার:

লিনিয়ার মানে সরলরেখা টাইপের। আমরা যদি সমস্যাটি একটা লাইনের মত মডেল দিয়ে সল্ভ করতে চাই তাহলে সেটা হবে লিনিয়ার মডেল।

সুতরাং লিনিয়ার রিগ্রেশন

তাহলে লিনিয়ার রিগ্রেশন হল লাইনের মত মডেল দিয়ে Real Value প্রেডিক্ট করার পদ্ধতি। যদি আমার মডেলটা ব্যাঁকাত্যাড়া লাইনের মাধ্যমে ভ্যালু প্রেডিক্ট করত তাহলে তার নাম হত Polynomial Regression।

Single Variable Linear Regression

আচ্ছা, ডায়বেটিস ডেটাসেট বিশ্লেষণ করার সময় আমরা বেশ কিছু ইনপুট ভ্যালু নিয়ে কাজ করেছিলাম যেমন no. of pregnencies, insulin level ইত্যাদি। **কিন্তু আপনার বন্ধু যে ডেটাসেট দিয়েছে তাতে ইনপুট কলাম মাত্র একটা বাড়ির সাইজ‍।

তাই আমরা এই সমস্যাকে Single Variable Linear Regression হিসেবে ভাগ করছি। যদি এখানে একটার বদলে আরও একটা ইনপুট ভ্যারিয়েবল থাকত, যেমন No of rooms থাকত তাহলে তাকে আমরা বলতাম Multi Variable Linear Regression Problem

এটা একটা Supervised Learning Problem

কারণ, আমরা এখানে সঠিক উত্তরসহ কিছু ডেটা দিচ্ছি, মানে আমরা অলরেডি কিছু বাড়ির আকার ও দাম জানি, সেটাই মেশিন লার্নিং মডেলে পাঠাব। লেবেলড ডেটা পাঠানোর মানেই হল সুপারভাইজড লার্নিং।

লিনিয়ার মডেলের মাধ্যমে প্রেডিকশন বলতে আসলে কী বুঝাচ্ছি?

আমরা ছোট একটা ডেটাসেটের এর মাধ্যমে বিষয়টা বোঝার চেষ্টা করি। ধরা যাক, আপনার নামীদামী রেস্টুরেন্টে খেতে যাওয়ার হার আপনার আয়ের সমানুপাতিক। আর আপনি এমন একটা কোম্পানিতে চাকরি করেন যেখানে আপনার বেতন মাসে মাসে বাড়ে (আছে নাকি এমন কোম্পানি?) ।

আপনি ৫ মাস চাকরি করার পর হিসেব করতে বসলেন আপনি ৫ মাসের, প্রতি মাসে কয়বার কেএফসি, বিএফসি, হাজীর বিরিয়ানি, স্টার কাবাব ইত্যাদি ইত্যাদিতে খেতে গিয়েছেন। হিসেব করার পর দেখলেন ডেটাসেট টা দাঁড়িয়েছে এইরকম।

প্রতি মাসে আয় (৳)	প্রতি মাসে কয়বার বাইরে খেতে গিয়েছেন
20k	5
30k	10
40k	15
50k	20
60k	25

আপনি যেহেতু এতক্ষণে matplotlib লাইব্রেরিতে ভালই হাত পাকিয়েছেন তাই ভাবলেন একটা গ্রাফ এঁকে ফেলা যাক।

import matplotlib.pyplot as plt
import numpy as np

beton = np.array([20, 30, 40, 50, 60])
khaoa = np.array([5, 10, 15, 20, 25])

plt.xlabel('Proti mash e income')
plt.ylabel('Khete jaoar har')

# আয় vs ব্যয় 
plt.title("Ae vs Bae")
plt.plot(beton, khaoa)
plt.show()

গ্রাফ

graph

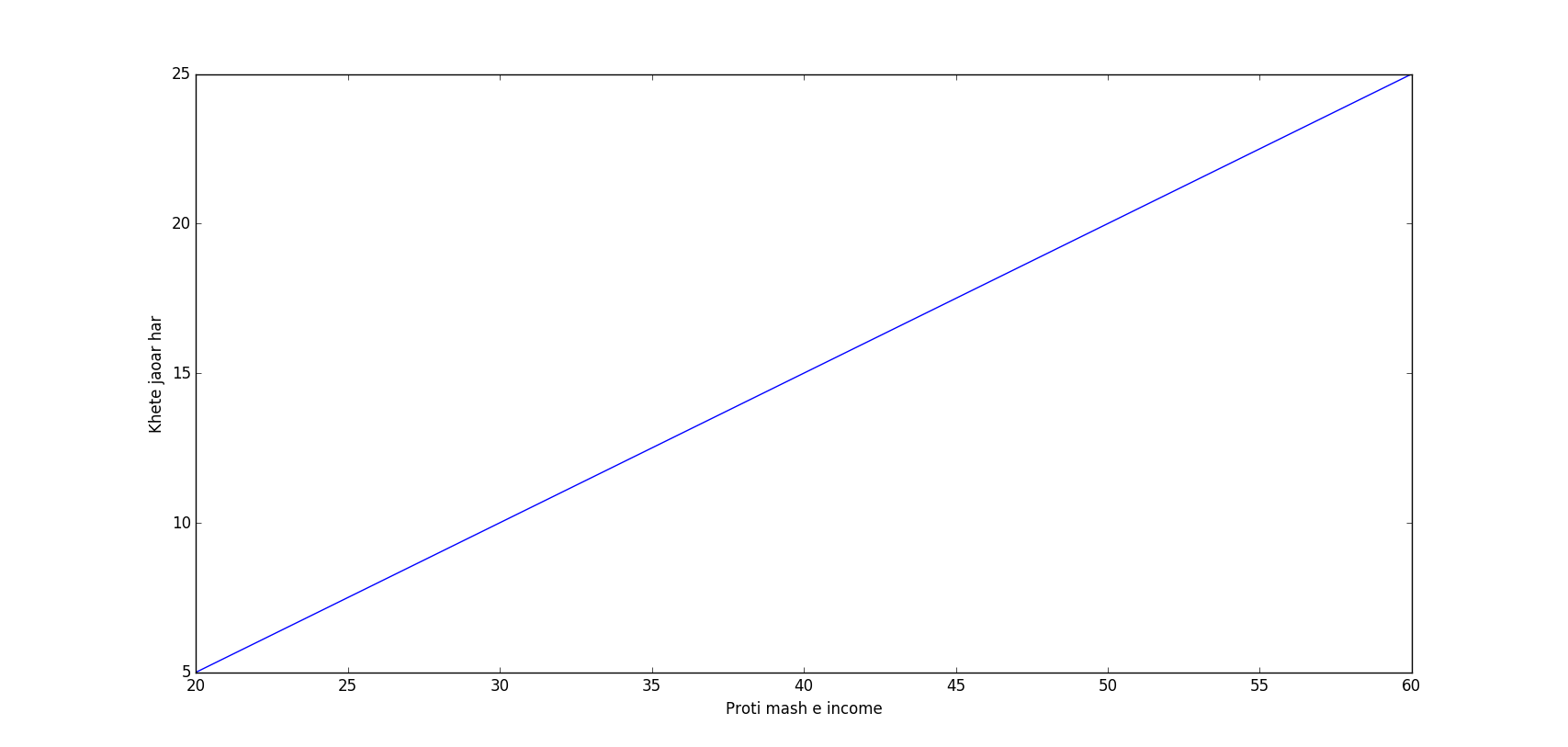
এবার যদি আপনাকে বলি, আচ্ছা বলেন তো, ৬ষ্ঠ মাসে আপনি কতবার বাইরে খেতে যাবেন? আপনি কষ্ট ছাড়াই বলে দিতে পারবেন, ৩০ বার (যদি আয় সুষমভাবে বাড়ে) ।

এইযে আপনি প্রেডিক্ট করলেন, সেটার কিন্তু একটা ম্যাথমেটিক্যাল মডেল তৈরি করা যায়।

$$ Khaoa = \frac{Aye - 10k}{10k} \times 5 $$

এই সমীকরণ দিয়ে আপনি ডেটসেট ভেরিফাই করতে পারেন।

এইখানে আমি একটা সমীকরণ তৈরি করলাম, এটাই হল সেই লিনিয়ার মডেল যেখানে আপনি Aye ইনপুট দিলে কয়বার বাইরে খেতে যাবেন সেটা প্রেডিক্ট করা যাবে। লিনিয়ার মডেল হওয়ার চাক্ষুষ প্রমাণ হল গ্রাফ। আপনার এই ডেটাসেট সন্দেহাতীত ভাবে লিনিয়ার মডেলে Fit করে যায়।

এবার আরেকটা সিনারিওর কথা চিন্তা করা যাক,

প্রতি মাসে আয় (৳)	প্রতি মাসে কয়বার বাইরে খেতে গিয়েছেন
20k	5
30k	10
40k	15
50k	20
60k	25
50k	25
40k	15
30k	2

এই ডেটাসেট এ দেখুন প্রথমদিকের মাসগুলোতে আপনার ইনকাম বাড়লেও পরবর্তীতে কমছে, প্রথম প্রথম আপনি বাইরে খেতে যাওয়ার অভ্যাস ছাড়তে পারেন নি। তারপর একদম বেশিই কন্ট্রোলে নিয়ে ফেলেছেন।

এই ডেটাসেট এর একটা স্ক্যাটার প্লট দেখা যাক,

scatter

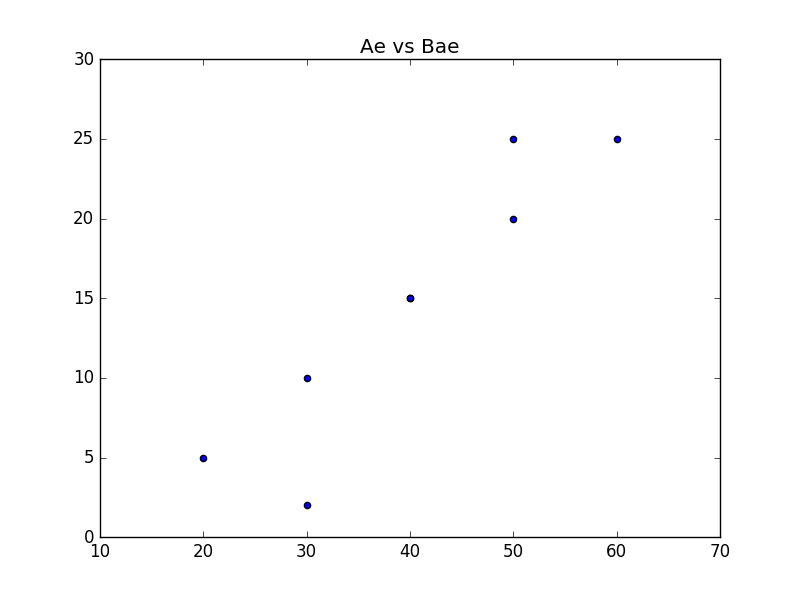
এইবার আপনাকে যদি বলি, পরের মাসে আপনার আয় যদি 15k তে নামে তাহলে আপনি কয় বার যাবেন? এখন আর ডেটাসেট এ লিনিয়ার প্যাটার্ন নেই, কোন স্পেসিফিক ইক্যুয়েশন ও নেই যার মাধ্যমে আপনি সহজেই প্রেডিক্ট করতে পারবেন।

আমরা হয়ত এক্সট্রিম কন্ডিশন ধরে নন লিনিয়ারিটি বাদ দিয়ে লিনিয়ার মডেল বসাতে পারি। সেটা পরের আলোচনা। এখন আমরা লিনিয়ার প্যাটার্ন নিয়েই আলোচনা করব। আমরা লিনিয়ার রিগ্রেশন বুঝলাম, এখন বুঝব মডেল রিপ্রেজেন্টেশন কী জিনিস।

মডেল রিপ্রেজেন্টেশন

মডেল রিপ্রেজেন্টেশন এর সহজ বাংলা হল, একটা ডেটাসেট এ আমরা যে বিশ্লেষণ চালাব, সেটার বিভিন্ন নোটেশন এর মানে কী, কিভাবে লেখে এবং কেতাবি গঠন কীরকম। এটার দরকার কেন? কারণ হল আপনি যখন মেশিন লার্নিংয়ের থিওরিটিক্যাল বই পড়তে যাবেন তখন এই কোর্সের সাথে মিল পাবেন না। সেখানে ম্যাথের হাবিজাবি সিম্বল দিয়ে মডেল রিপ্রেজেন্ট করা থাকতে পারে। তাই সেগুলো বোঝার জন্য আমাদের অফিশিয়াল নোটেশন সম্পর্কেও জানা দরকার।

আপনার বন্ধুর দেওয়া ডেটাসেট টা আবার একটু দরকার তাই এখানে আরেকবার পেস্ট করলাম।

বাড়ির সাইজ (একক - sq ft) (ধরি এটা X)	বাড়ির দাম (একক - ৳) (ধরি এটা, Y)
2104	399900
1600	329900
----	----
1852	299900
1203	239500

এই ডেটাসেট এর Row সংখ্যা 47 তাই আমরা লিখব,

m = 47
X = "input" variable / feature  
Y = "output" variable / "target" value

$$ (x, y) $$ এই নোটেশন দিয়ে একটা Row বোঝানো হয়, সেটা যেকোন টা হতে পারে।

আমি যদি 20 তম Row বুঝাতে চাই সেক্ষেত্রে আমি লিখব $$ (X^{(20)}, Y^{(20)}) $$।

তারমানে $i^{th}$ training example বুঝাতে হলে বলতে হবে $(X^{(i)}, Y^{(i)})$

হাইপোথিসিস

একটা ডায়াগ্রাম দেখা যাক,

hypothesis

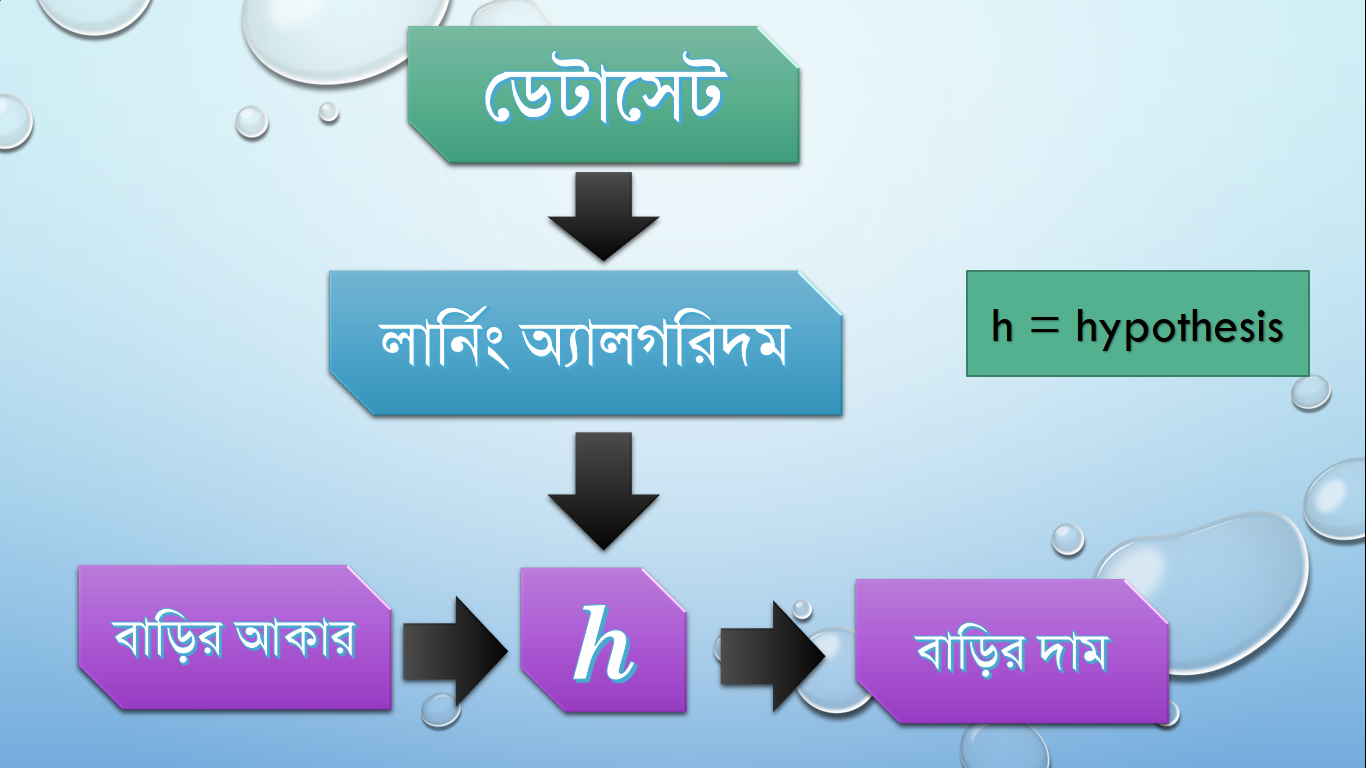
প্রশ্ন হল,

এই $h$ আমরা কীভাবে তৈরি করব? যেহেতু আজকের চ্যাপ্টারটি লিনিয়ার মডেল নিয়ে তাই ধরা যেতে পারে আমরা $h$ একটা লিনিয়ার ফাংশন বাছাই করব।

ধরি আমাদের Hypothesis হচ্ছে, $h_{0}(x) = \theta_{0} + \theta_{1} \times x$ শর্টহ্যান্ডে আমরা $h_{0}$ কে $h$ লিখে থাকি। লক্ষ্য করে থাকবেন এখানে ইনপুট ভ্যারিয়েবল মাত্র একটা, তাই একে আমরা বলব Univariate Linear Regression।

কস্ট ফাংশন (Cost Function)

আমরা সাধারণত আয় হিসেব করে ব্যয় করি। সবসময় চেষ্টা করি যাতে আমাদের ব্যয় সর্বনিম্ন হয়। মেশিন লার্নিংয়ের ক্ষেত্রে ঠিক তাই করা হয়। এখানে সর্বাত্মক চেষ্টা থাকে, Cost Function কতটা মিনিমাইজ করা যায়। মডেল ট্রেইনিং বলতে আমরা বুঝি Cost Function Minimization।

কস্ট ফাংশন মিনিমাইজ করার আগে বুঝতে হবে Cost Function দ্বারা আসলে কী বোঝায়। Cost Function বোঝার আগে আরেকটা জিনিস জেনে নেওয়া যাক।

আমরা হাইপোথিসিস এর জন্য যে ফাংশনটি বাছাই করেছি $h_{0}(x) = \theta_{0} + \theta_{1} \times x$ । এখানে শুধু আমরা $x$ এর মান জানি। কিন্তু $\theta_{0}$ এবং $\theta_{1}$ এর মান কত হবে সেটা জানিনা। চলুন সেটার মান কী হবে তা নিয়ে একটু গবেষণা করা যাক।

একটা কাজ করি আগে, আপনার বন্ধুর দেওয়া ডেটাসেট এর একটা স্ক্যাটার প্লট এঁকে ফেলি।

scatter_plot

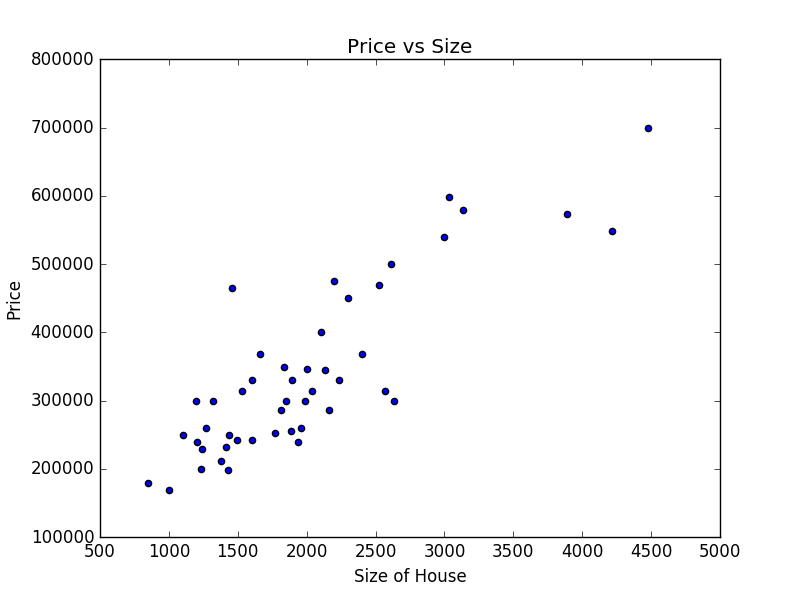
আমাদের যেটা করতে হবে এইরকম একটা স্ট্রেইট লাইন এই ডেটার মধ্যে Fit করতে হবে।

scatter_plot_fitline

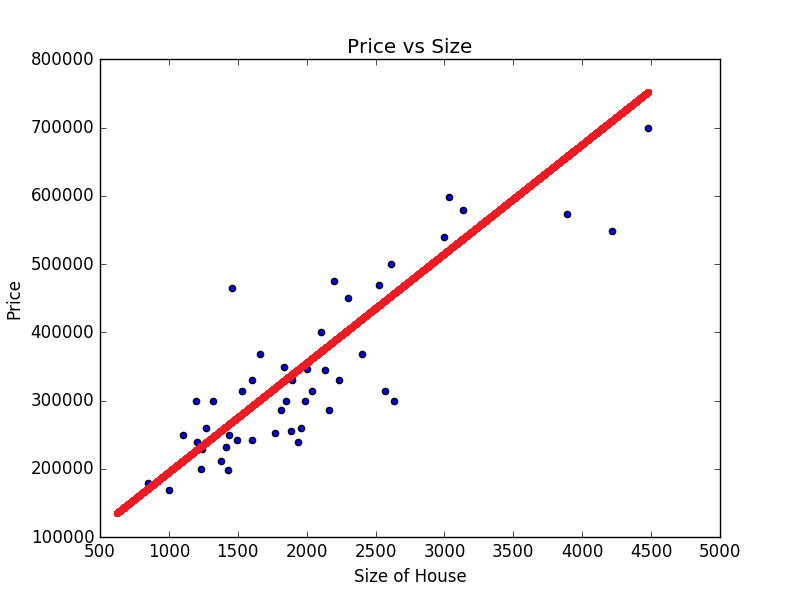
তারমানে $\theta_{0}$ এবং $\theta_{1}$ এর মান এমনভাবে বাছাই করতে হবে যেন আমাদের hypothesis এর মান (প্রেডিকশন) ডেটাসেট এর মানের কাছাকাছি হয় অর্থাৎ খরচ সবচেয়ে কম হয় বা Cost Function Minimized হয়।

থিটা এর মান কিরকম হলে সেটা ডেটাসেট এ ফিট করবে সেটা জানার আগে আমাদের দেখতে হবে প্যারামিটার (থিটা গুলো) এর মান পরিবর্তনের সাথে সাথে h এর গ্রাফ কীরকম আসে।

ধরি এবং

তাহলে গ্রাফ আসবে এইরকম,

scatter1

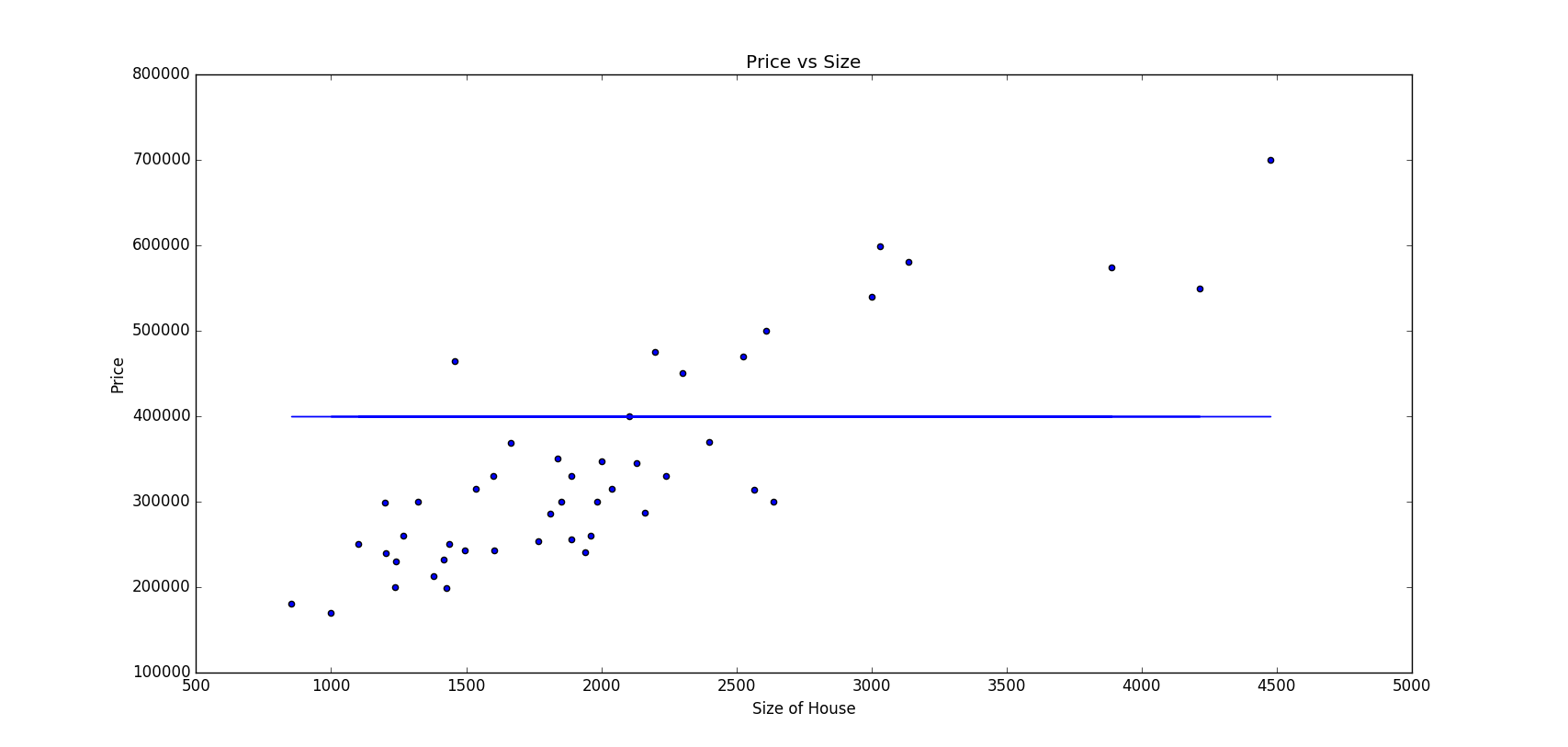
ধরি এবং

তাহলে গ্রাফ আসবে এইরকম,

scatter2

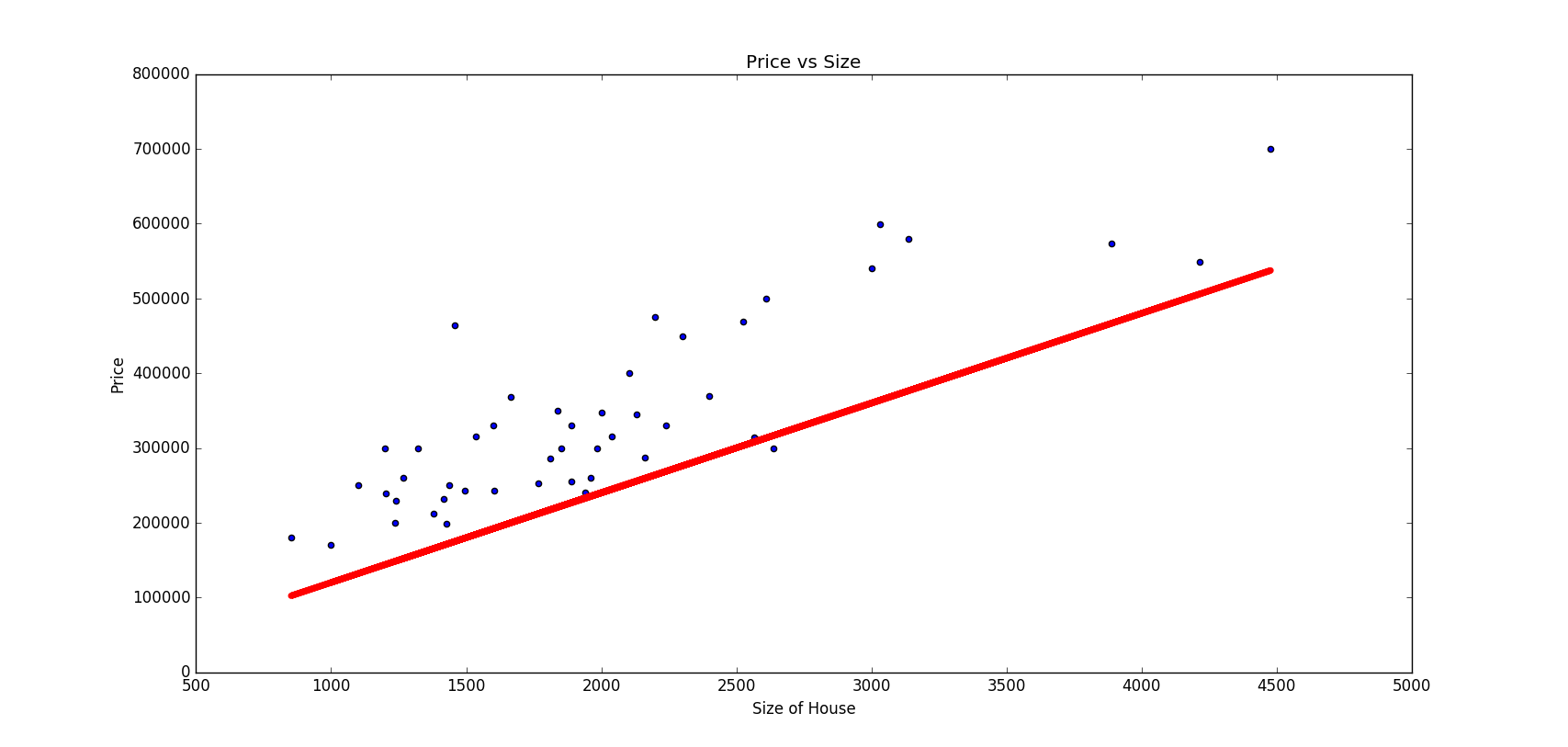
ডেটাসের এর সাথে কিন্তু প্রায় ফিট করে গেছে। আমাদের যেটা করতে হবে লাইনটা আরেকটু শিফট করে উঠাতে হবে, $y = mx + c$ এর কথা মনে আছে না? $m$ হল ঢাল আর $c$ হল ধ্রুবক যার কাজ স্ট্রেট লাইন কে Y-Axis এর পজিটিভ দিকে উঠিয়ে দেয়া ($c$ এর পজিটিভ মানের জন্য)।

এখানে $\theta_{0}$ আসলে সেই $c$ এর কাজ করছে এবং $\theta_{1}$ করছে $m$ এর কাজ।

এবার আমরা দুইটা প্যারামিটার ব্যবহার করে আবার গ্রাফ প্লট করার চেষ্টা করি।

ধরি, এবং

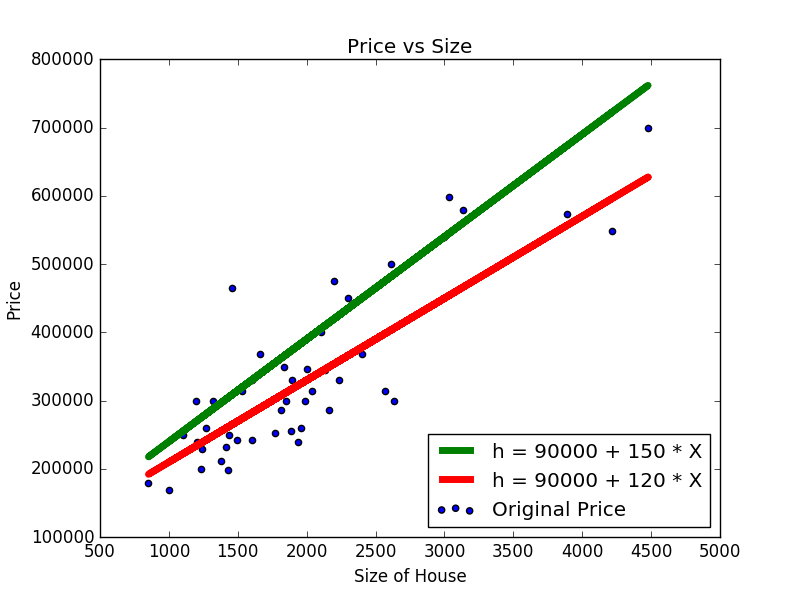
আমাদের হাইপোথিসিস হয়, $h = 90000 + 120 \times x$

এইবার প্রতি বাড়ির সাইজের জন্য আমাদের হাইপোথিসিস এর আউটপুট এর স্ট্রেইট লাইন প্লট ও স্ক্যাটার প্লটের আউটপুট কম্পেয়ার করে দেখা যাক

hypo3

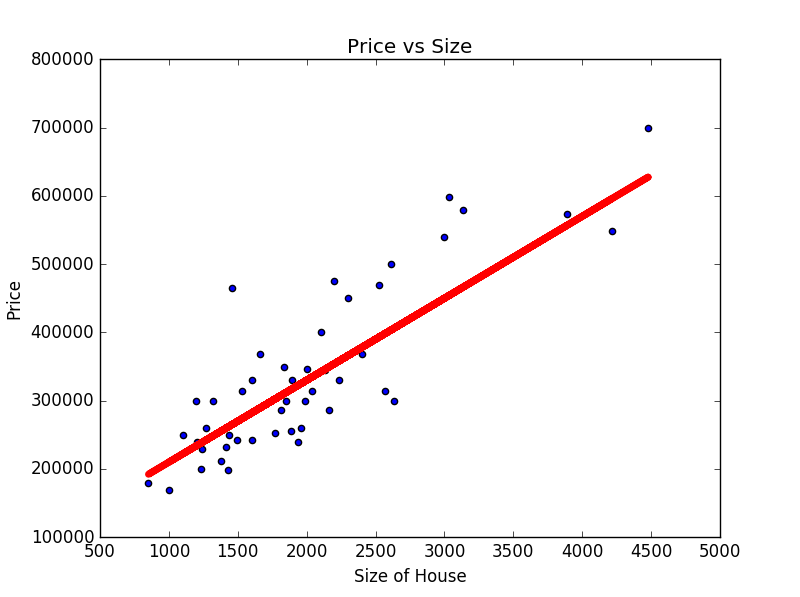
বলতেই হবে বেশ ভালই এসেছে (দৃশ্যত)। কিন্তু দেখুন উপরের দিকে কিছু ডেটা বাদ পড়ে গেল, তারমানে আমরা $\theta_{0}$ ও $\theta_{1}$ আরেকটু টিউন করে এইরকম গ্রাফ পেতে পারি,

সবুজ রংয়ের লাইনটা আমাদের নতুন হাইপোথিসিস। লাল রংয়ের লাইনটা হচ্ছে আগের।

hypo4

সব ই বুঝলাম কিন্তু কস্ট ফাংশনটার কথা বললেন না? সেইটার টিকিটাও পাচ্ছি না।

চিন্তার কিছু নাই, আমরা হাইপোথিসিস দাঁড়া করিয়েছি এইবার আমরা কস্ট ফাংশন দেখব।

Cost Function কে $J(\theta_{0}, \theta_{1})$ দ্বারা প্রকাশ করা হবে এখানে, যদি আমাদের মডেলে আরও কয়েকটা থিটা থাকত যেমন $\theta_{2}, \theta_{3} ...$ ইত্যদি তাহলে আমরা কস্ট ফাংশন প্রকাশ করতাম $J(\theta_{0}, \theta_{1} , \theta_{2} ,\theta_{3}, ...)$ ইত্যাদি। তারমানে Cost Function এর প্যারামিটার আর মডেল প্যারামিটার একই হবে।

Cost Function এর সূত্র হল,

$J (\theta_{0}, \theta_{1}) = \frac{1}{2m} \sum_{i=1}^{m} \left ( h_{0} ( X^{(i)}) - Y^{(i)} \right )^{2}$

মনে আছে তো কোনটা কি? না মনে থাকলে শুরু থেকে পড়ে নিন। আমি এখানে Cost Function হিসেবে Ordinary Least Square মেথড অ্যাপ্লাই করেছি। Cost Function যে শুধু এটাই হবে তা নয়। তবে সাধারণত এইটা ব্যবহার করা হয়।

কস্ট ফাংশন যেটা বলতে চায়, সেটা হল; আমরা প্রতি Observation এর জন্য Error বের করব (Error = Hypothesis Value - Real Value), সেই Error কে বর্গ করব। এভাবে প্রতি $Error^{2}$ এর যোগফল বের করব (m সংখ্যক $Error^{2}$ এর যোগফল)। তারপর তাকে $\frac{1}{2 \times m}$ দিয়ে ভাগ দিব।

কথা না বাড়িয়ে আমরা ডেটাসেট এর 5 টি অবজারভেশনের জন্য Cost ক্যালকুলেট করি।

ডেটাসেট এর প্রথম পাঁচটি Observation

বাড়ির সাইজ (একক - sq ft) (ধরি এটা X)	বাড়ির দাম (একক - ৳) (ধরি এটা, Y)
2104	399900
1600	329900
2400	369000
1416	232000
3000	539900

ধরি আমাদের Hypothesis, $h = 90000 + 120 \times X$

Input,
X = [2104, 1600, 2400, 1416, 3000]

Real output,
Y = [399900,329900, 369000, 232000, 539900]

Hypothesis output,

Example, 
h1 = 90000 + 120 * 2104 = 342480
h2 = 90000 + 120 * 1600 = 282000
....
h5 = 90000 + 120 * 3000 = 450000

H = [342480, 282000, 378000, 259920, 450000]

তাহলে বোঝা গেল কীভাবে মডেল প্যারামিটারের ভ্যালু ধরে নিয়ে আমরা হাইপোথিসিস ফাংশন দিয়ে ভ্যালু প্রেডিক্ট করলাম।

ভাল করে দেখুন Real ও Predicted ভ্যালু কাছাকাছি হলেও বেশ এরর আছে, আমরা সেই এরর এর উপর ভিত্তি করে Cost Calculate করব।

Real Value (Y)	Predicted Value (H)
399900	342480
329900	282000
369000	378000
232000	259920
539900	450000

এখানে Observation বা m = 5, কস্ট ফাংশন এর আউটপুট একটু ভেঙ্গে ভেঙ্গে লেখা যাক,

$J (90000, 120) = \frac{1}{2 \times m} \times ( e_{1}^{2} + e_{2}^{2} + e_{3}^{2} + e_{4}^{2} + e_{5}^{2} )$

যেখানে, $e_{1} = ( h(X^{1}) - Y^{1} ) = 342480 - 399900 = -57420$

এভাবে আমরা বাকি এরর গুলো পাইথন দিয়ে বের করে, সূত্র বসিয়ে Cost Calculate করব।

$e_{1}^{2} + e_{2}^{2} + e_{3}^{2} + e_{4}^{2} + e_{5}^{2} = 14534002800$

এবার $\frac{1}{2 \times m}$ দিয়ে গুণ করে,

$J (90000, 120) = 1453400280$

এটা হল $\theta_{0} = 90000, \theta_{1} = 120$ এর জন্য ক্যালকুলেটেড কস্ট।

এভাবে আমাদের বিভিন্ন $\theta_{0}, \theta_{1}$ এর কম্বিনেশনের জন্য Cost ক্যালকুলেট করে দেখতে হবে সর্বনিম্ন কস্ট কোন কম্বিনেশনে আসে, তারপর সেই কম্বিনেশন দিয়ে আমরা লিনিয়ার মডেল বানিয়ে পার্ফর্মেন্স টেস্ট করব।

সচরাচর জিজ্ঞাস্য প্রশ্ন:

Cost Function এ $\frac{1}{2}$ দিয়ে গুণ করার মানে কী?

এটা করা হয় পরবর্তী ম্যাথমেটিক্যাল ক্যালকুলেশন সহজ করার জন্য। আর কিছুই নয়। আপনি হাফ দিয়ে গুণ না করলেও সমস্যা নাই।

Residual, MSE (Mean Square Error), OLS (Ordinary Least Square), Loss Function, Residual Sum of Squares (RSS) কোনটার মানে কী?

• Residual এর মানে সবকয়টি Observation এর প্রডিক্টেড ভ্যালু আর আসল ভ্যালুর পার্থক্যের যোগফল। Error এর সমষ্টি বলতে যা বুঝায়, তা-ই।

• MSE বলতে সবকয়টি Observation এর Error এর বর্গের সমষ্টি বুঝায়

• Ordinary Least Square হল Statistical Estimator, যার সাহায্যে Cost ক্যালকুলেট করছি

• Loss Function হল Cost Function এর আরেকটা নাম বা Alias

• RSS এর সূত্র হল $RSS = \sum_{i=1}^{m}Residual^{2}$

Cost Function এর মেথড হিসেবে OLS ব্যবহার করা হয়েছে কেন?

খুবই গুরুত্বপূর্ণ একটি প্রশ্ন এবং সচরাচর জিজ্ঞাস্য নয়। Cost Function হিসেবে OLS ব্যবহার করার মূল কারণ $y = x^{2}$ এর গ্রাফ Parabolic হয়। প্যারাবলিক ফাংশন থেকে Cost Estimation করাটা খুবই সহজ। আর $Error^{2}$ এর গ্রাফ প্যারাবলিক হবে সেটাই স্বাভাবিক।

পরবর্তী পর্বে আমরা কস্ট ফাংশনের আরো ইনটুইশন দেখব এবং সমস্যা যদি মাল্টিভ্যারিয়েবলের হয় তাহলে লিনিয়ার মডেল দিয়ে কীভাবে রিপ্রেজেন্ট করতে হয় সেটা সম্পর্কেও জানব।