ডেটা প্রিপ্রেসসিং - শেষ পর্ব

“Organize, don't agonize.” ― Nancy Pelosi

ডেটা প্রস্তুত করা (ডেটা প্রিপ্রসেসিং) - ২

ডেটাফ্রেম পরিবর্তন করা

প্রায় সময়ই ডেটাসেটে ডেটা মিসিং থাকতে পারে। আমাদের সেই মিসিং ডেটাও হ্যান্ডেল করতে হবে। হ্যাঁ, হয়ত আমরা হারানো ডেটা পাব না, তবে প্রয়োজনীয় ব্যবস্থা না নিলে প্রোগ্রাম ক্র্যাশ করতে পারে।

কোন কোন Column বাদ দিতে হবে?

• যেগুলো ব্যবহার করা হবে না

• কলাম আছে কিন্তু ডেটা নাই

• একই কলাম যদি একাধিকবার থাকে, তাহলে একটা রেখে বাকিগুল‌ো মুছে দিতে হবে

  • অনেক সময় নাম দেখে মনে হতে পারে দুইটা আলাদা কলাম কিন্তু আসলে জিনিসটা একই। উদাহরণ হিসেবে বলা যায়, একটা কলামে লেখা আছে Length (meter) এবং আরেকটি কলামে লেখা আছে Size (centimeter), হঠাৎ দেখলে মনে হবে দুইটা জিনিস আলাদা কারণ লেবেল হচ্ছে Size ও Length। কিন্তু ভাল করে লক্ষ করে দেখা গেল, Length এর প্রত্যেকটা ডেটাকে 100 দিয়ে গুণ করে আমরা Size এর ডেটাগুলি পেয়ে যাচ্ছি। হাতে ক্যালকুলেশন করে একই ধরণের ডেটা বের করা সম্ভব হয় না এবং হলেও এটা কোন এফিশিয়েন্ট পদ্ধতি না। এই অতিরিক্ত কলামগুলো আসলে ডেটাসেট এ নয়েজ জেনারেট করে। আমরা স্ট্যাটিস্টিক্যাল অ্যানালাইসিস (এখানে Correlation) এর মাধ্যমে একই রকম কলামগুলি আলাদা করব।

Correlated Column কী?

• একই তথ্য যদি একটু ভিন্ন ফরম্যাটে থাকে, উপরের উদাহরণে Length এবং Size আসলে একই জিনিস, শুধু Unit আলাদা। তারমানে এরা Correlated Column।

• অল্প ইনফরমেশন অ্যাড করে বা করেই না।

• লার্নিং অ্যালগরিদমকে কনফিউজ করে।

লিনিয়ার রিগ্রেশন নিয়ে অল্প কিছু কথা

পরবর্তী উদাহরণ বুঝতে গেলে আমাদের লিনিয়ার রিগ্রেশন এর কিছু বেসিক লাগবে।

নিচের কাল্পনিক ডেটাসেট এর কথা চিন্তা করা যাক,

House Size (sq ft)	Price (Tk in lac)
1	5
2	10
3	15
4	20

গ্রাফ

graph

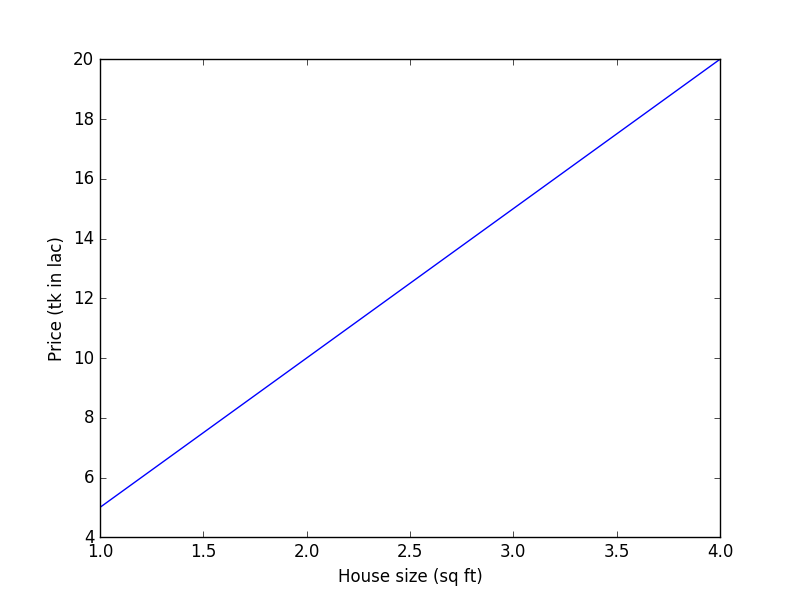
আপনাকে যদি বলা হয়, 5 sq ft বাড়ির দাম কত হবে? আপনি নির্দ্বিধায় বলে দিতে পারবেন, উত্তর হবে 25 lac।

কীভাবে বললেন?

খুব সহজ, প্রতি ‍1 sq ft বৃদ্ধির জন্য দাম বাড়ছে 5 lac করে।

আমরা যদি একটা ম্যাথেমেটিক্যাল মডেল দাঁড়া করাতে চাই, সেটা হবে অনেকটা এরকম।

$price = size (sqft) \times 5 (tk in lac)$

বা,

$y = f(x) = \alpha \times x$

যেখানে, $y$ হচ্ছে প্রাইস, $x$ হচ্ছে সাইজ $\alpha$ হচ্ছে 5 এবং $f(x)$ ফাংশনটি বলে দিচ্ছে $x$ এর মানের জন্য প্রাইস কত হবে

বাস্তবে মডেল এতটা সহজ হয় না, অনেক প্যাঁচ থাকে, এখন আমি একটা alpha গুণ দিয়েই মান পেয়ে যাচ্ছি তখন beta, gamma, theta হাবিজাবি যা আছে তা দিয়ে গুণ দিলেও হয়ত কাছাকাছি মান পাবেন না।

নিচের ডেটাসেট দেখা যাক,

House Size (sq ft)	No of rooms	Price (tk in lac)
1	3	10
2	3	12
3	4	14
4	4	17
5	5	22

গ্রাফ

graph2

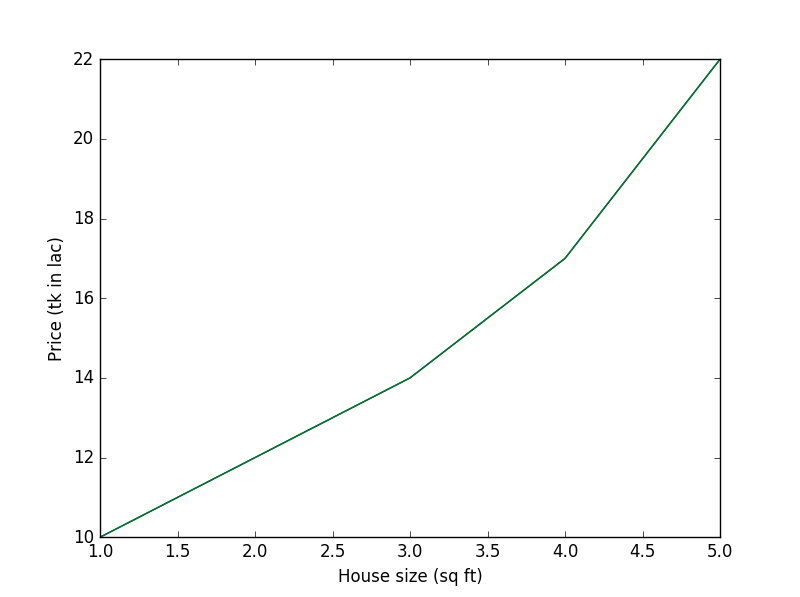
এবার আপনাকে যদি বলি, বাড়ির আকার যদি 6 sq ft হয় তাহলে প্রাইস কত হবে? এবার আপনি বেশ ঝামেলায় পড়ে যাবেন, কারণ প্রতি স্কয়ার ফিট আকার বৃদ্ধির সাথে বর্ধিত দাম সুষম নয়। আগেরটা বিয়োগ দিয়ে পার্থক্য বের করে সেটার সাথে পার্থক্য যোগ করে পরের প্রাইস পেয়ে যাবেন, সমস্যাটা এত সহজ নয়। কারণ সাথে আবার যুক্ত হয়েছে No of rooms।

এখন যদি আমাকে বলা হয়, এটার একটা ম্যাথেমেটিক্যাল মডেল দাঁড়া করাতে তাহলে আমিও বেশ ঝামেলায় পড়ে যাব। এমন কোন সেই লিনিয়ার ইক্যুয়েশন, যেটাতে 1, 2, ... 5 ইনপুট দিলে যথাক্রমে 10, 12 ... 22 পাওয়া যায়?

এক্স্যাক্ট কোন মডেল বিল্ড না করতে পারলেও হয়ত কাছাকাছি কোন মডেল তৈরি করতে পারব যার ইক্যুয়েশন অনেকটা এরকম হতে পারে,

$price = \alpha \times size + \beta \times rooms$

Correlated Column এর উদাহরণ

ধরা যাক, আমরা আবারও সেই বিখ্যাত সমস্যা House Price Prediction টা আলোচনায় আনি।

House Area (Acre)	Size (kilo sq meter) (approx.)	No of rooms	Price (tk in lac)
1	4	3	10
2	8	4	12
3	12	4	16

ডেটাসেট এর কলাম ভালভাবে পরীক্ষা না করেই প্রেডিক্ট করতে বসে গেলাম নিচের ফরমুলা (Linear Regression ফরমুলা) দিয়ে,

$Price = \alpha * Area \, (Acre) + \beta \times Size(kilo \, sq \, meter) + \gamma \times noOfRooms$

আমরা লিনিয়ার রিগ্রেশনের ক্ষেত্রে দেখেছিলাম প্রত্যেকটা ফিচার (ইনপুট ভ্যারিয়েবল) কে একটা Co-efficient দিয়ে গুণ করি তারপর সেগুলোকে যোগ করে আউটপুট প্রেডিক্ট করি। একই রকম কলাম Area & Size দুইবার রাখার কারণে আউটপুট Price কখনোই ঠিকঠাক আসবে না।

এখানে কলাম দুইটা একই রকম সেটা সহজে বোঝা যাচ্ছে কারণ উদাহরণটা আমার তৈরি করা :P । জোক্স অ্যাপার্ট, যদি অনেকগুলো কলাম হয়, আর সবগুলার নাম আলাদা হয় আর ডেটাও আলাদা হয় কিন্তু আসলে একটা আরেকটার ইউনিট বেজড সিনোনিম হয় সেগুলো বের করা অনেক জটিল ব্যবহার। তাই আমরা এখানে পরিসংখ্যানের একটি গুরুত্বপূর্ণ টপিক (Correlation) এর সাহায্য নেব।

Pearson's Correlation Co-efficient বা Pearson's r

Pandas লাইব্রেরিতে কো-রিলেশন ফাংশন কল করলে সেটা নিচের সূত্রানুযায়ী কো-রিলেশন ক্যালকুলেট করে। কো-রিলেশন নিয়ে বিস্তারিত আলোচনা আরও করা হবে, আপাতত এই ফরমুলা নিয়ে খুশি থাকুন।

pearson_formula

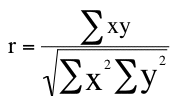
এই ফরমুলায়, x হচ্ছে একটা ভ্যারিয়েবল আর y হচ্ছে আরেকটা ভ্যারিয়েবল (Isn't it too obvious?)।

আমাদের বের করতে হবে r এর মান কত। r এর মান দিয়ে আমরা বুঝতে পারি যে দুইটা ভ্যারিয়েবলের সামঞ্জস্যতা কতখানি। যদি r = 1 হয় তারমানে দুইটা ভ্যারিয়েবলের মধ্যে কোন পার্থক্য নাই, তাই যেকোন ভ্যারিয়েবলের নিজের সাথে কো-রিলেশন ক্যালকুলেট করলে r এর মান হয় 1

আরও ব্যাখ্যা যদি চান, উপরের উদাহরণের Acre এবং Sq meter এর মধ্যকার Correlation Co-efficient ক্যালকুলের করলে r এর মান 1 পাবেন।

প্রমাণ: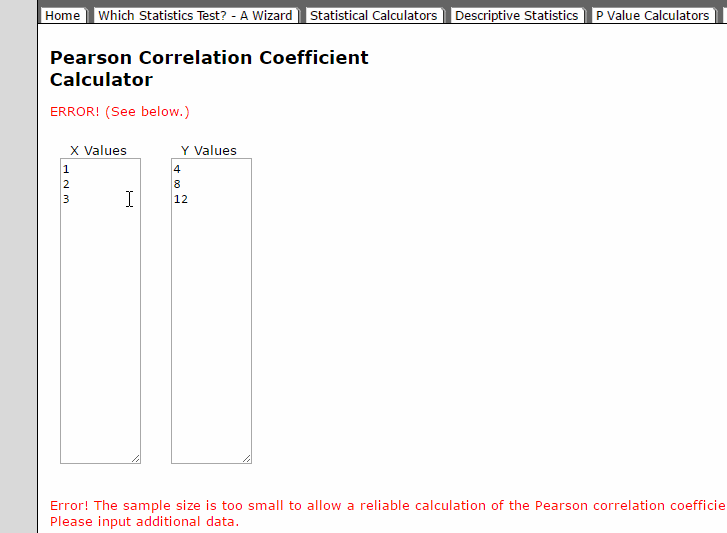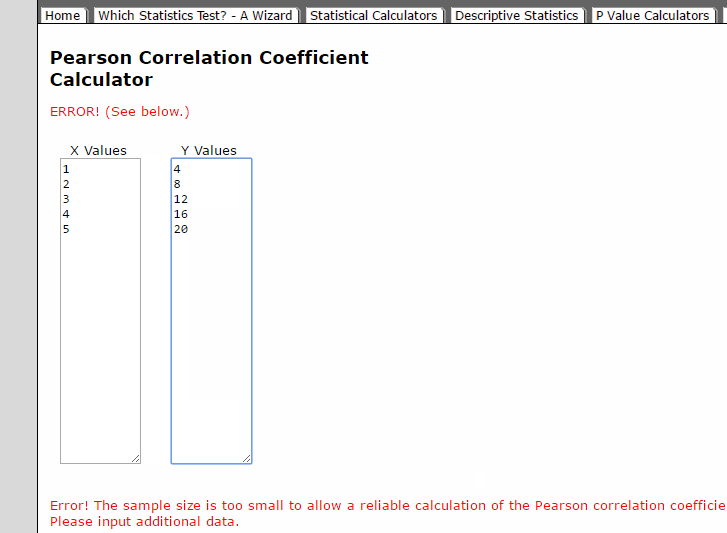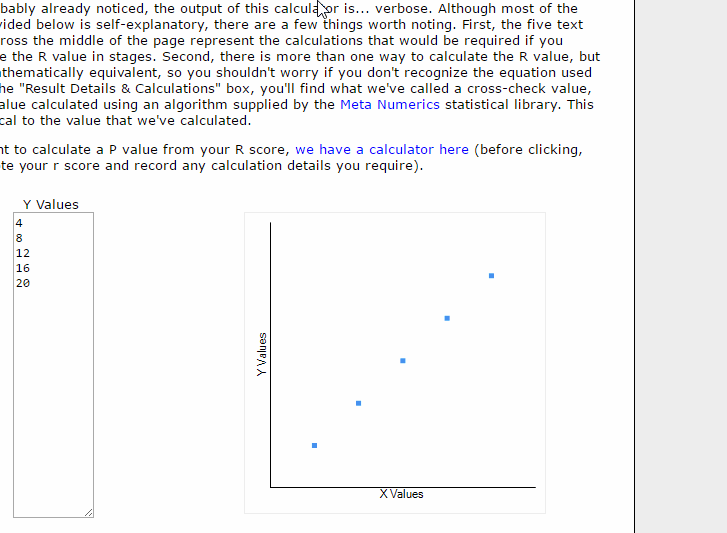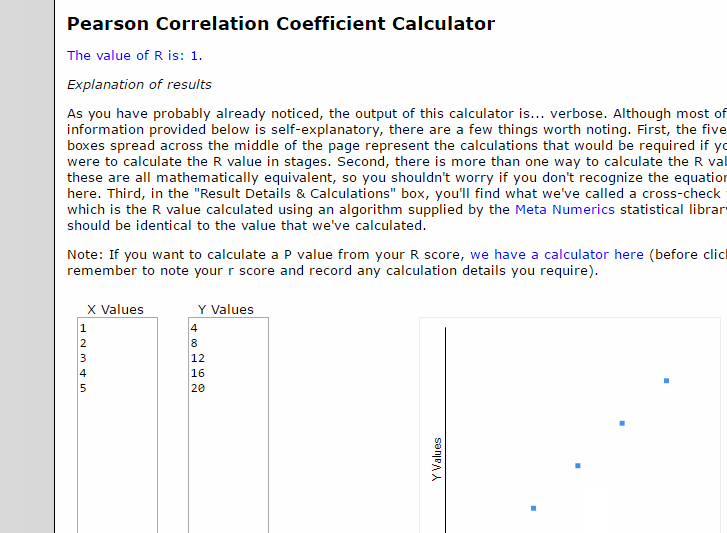

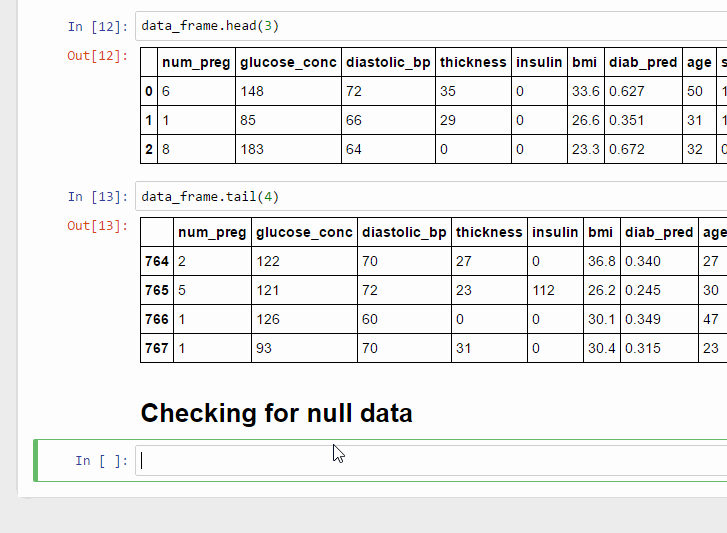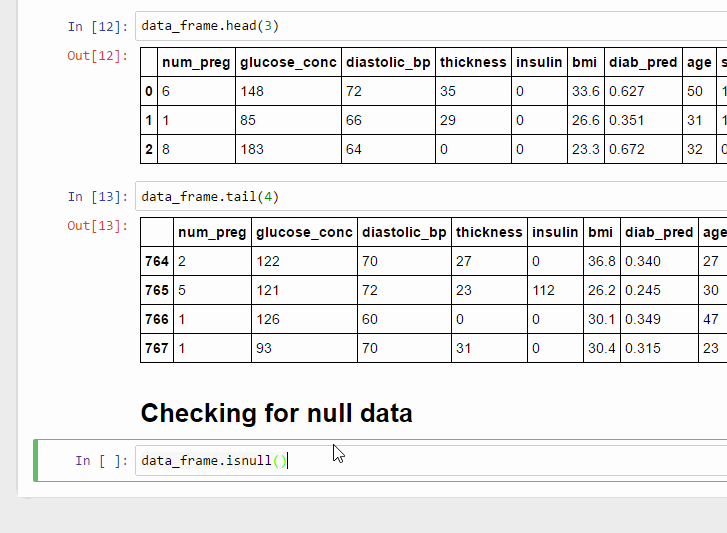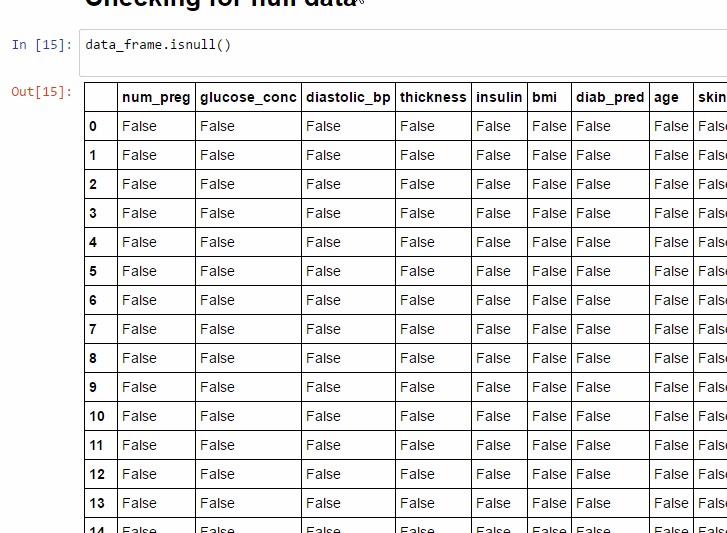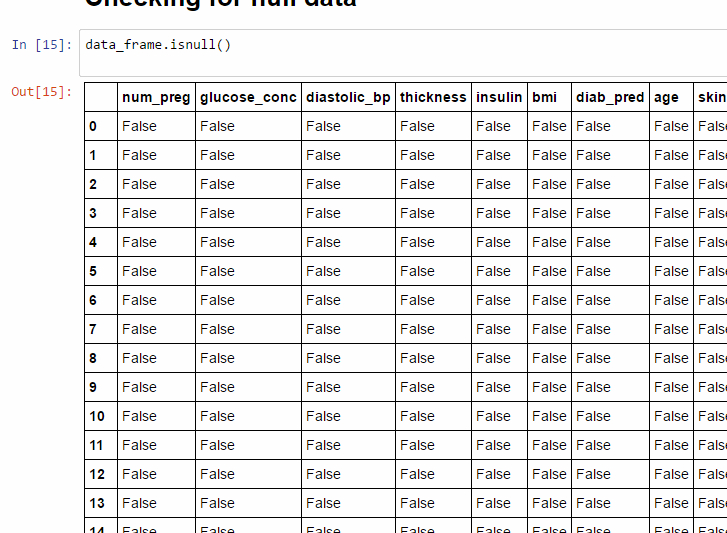
এবার দেখা যাক ডেটাসেটের কোন কলামে কোন ডেটা মিসিং আছে কিনা সেটা কীভাবে বের করা যায়।

Null বা ডেটাসেট এর ফাঁকা অংশ বের করা

আগের তৈরি করা নোটবুক ওপেন করুন আর নিচের কোডটি লিখুন,

print data_frame.isnull().values.any()

isnull().values.any()

isnull()

এটা আবার সেই ডেটাফ্রেমকেই রিটার্ন করে কিন্তু পার্থক্য হল সেখানে আর ভ্যালু থাকে না, Empty Cell রিপ্লেস হয় True দিয়ে আর Non-Empty Cell রিপ্লেস হয় False দিয়ে।

checkdata1

values.any()

checkdata2

isnull() রিটার্ন করে ডেটাফ্রেম, কিন্তু .values দিলে সেটা True/False এর একটা অ্যারে তে পরিণত হয়।

‍.any() ফাংশন চেক করে অ্যারেতে থাকা কোন ভ্যালু ফাঁকা বা Empty কিনা।

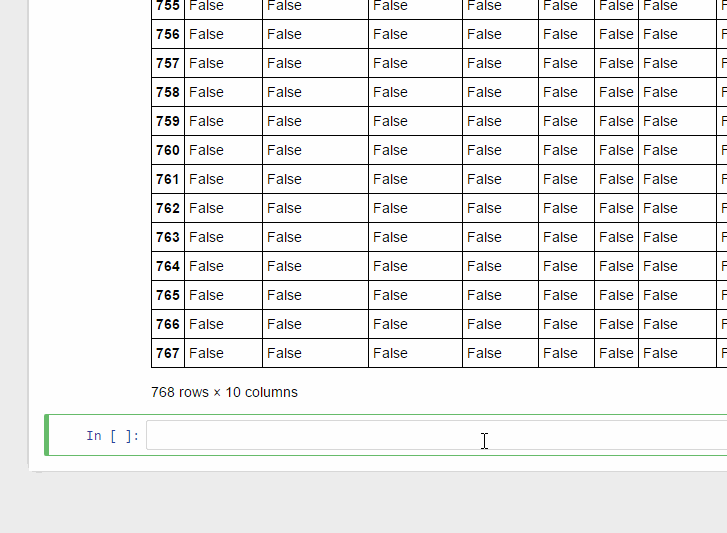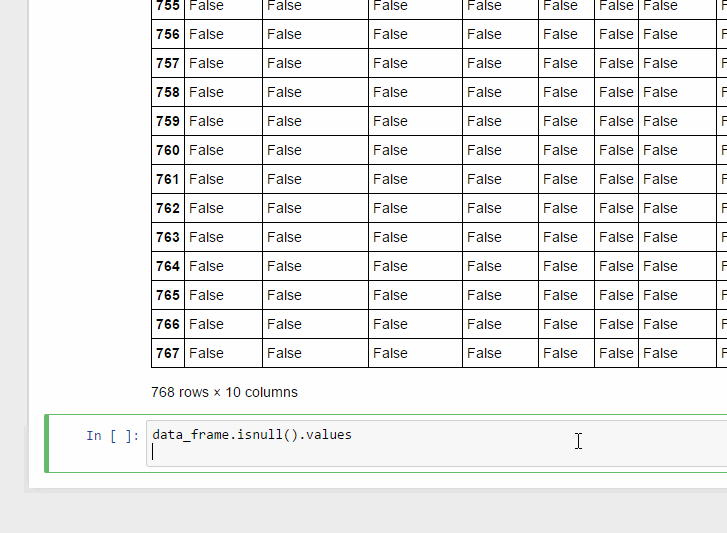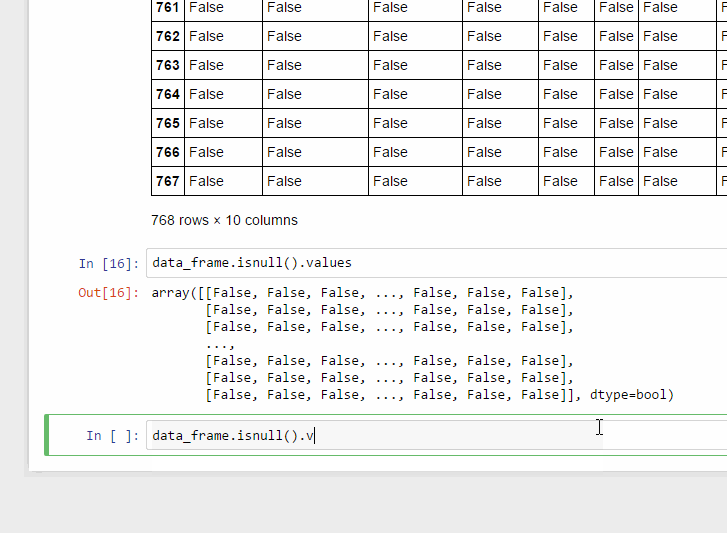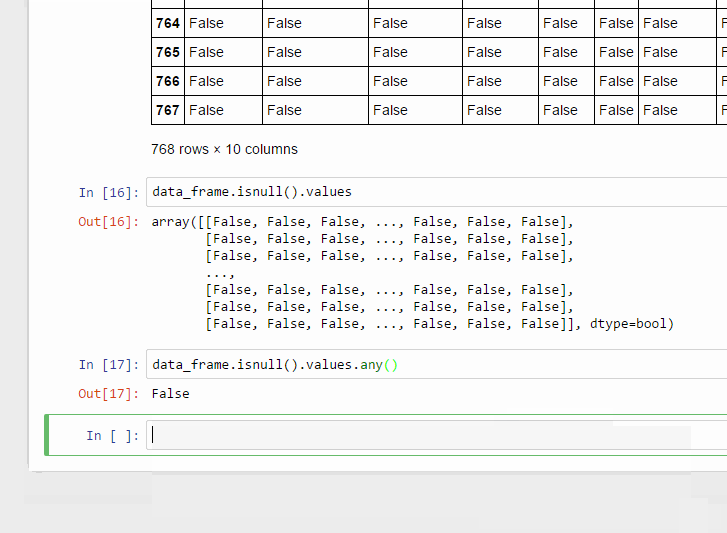
pima-data.csv ফাইলে কোন ফাঁকা ডেটা নাই। তাই এই প্রোগ্রাম স্টেটমেন্টটি কল করলে False দেখায়।

ইচ্ছাকৃত একটা Cell ডিলেট করে আবার data_frame.isnull().values.any() স্টেটমেন্ট রান করা

এখানে আমি pima-data.csv ফাইলের একটা সেল ইচ্ছে করে ডিলেট করে আবার Pandas দিয়ে লোড করে কোডটা চালিয়ে দেখলাম।

দেখা যাচ্ছে এখন আউটপুট আসছে True। তারমানে কোন না কোন একটা সেল খালি আছে।

checkdata3

Correlation Matrix Heatmap তৈরি করা

আমরা এতক্ষণে Correlation সম্পর্কে কিছুটা জানলাম আর দেখলাম ডেটাসেট এ কোন Null ভ্যালু লুকিয়ে থাকলে সেটাকে কীভাবে বের করা যায়। এখন দেখব, কীভাবে Correlation Matrix Heatmap জেনারেট করতে হয়। তার আগে একটু বলা যাক, Heatmap টা কী জিনিস।

Heatmap

উইকিপিডিয়া অনুসারে,

A heat map (or heatmap) is a graphical representation of data where the individual values contained in a matrix are represented as colors.

অর্থাৎ, নিউমেরিক্যাল ভ্যালু আমরা রং দিয়ে রিপ্লেস করে একটা প্লট জেনারেট করি। সেটাই হবে Heatmap।

তারমানে, Correlation Heatmap হচ্ছে Correlation ভ্যালুগুলোকে রং দিয়ে রিপ্লেস করে গ্রাফে প্লট করা।

Correlation Heatmap

আমরা দেখেছি, দুইটা ভ্যারিয়েবলের মধ্যে কো-রিলেশন ক্যালকুলেট করে কীভাবে

আপনি নিজেই নিজেকে প্রশ্ন করে দেখুন, কতগুলা ভ্যালু (ফ্লোটিং পয়েন্ট) কে তুলনা করা সহজ নাকি রং তুলনা করা সহজ? অবশ্যই রং তুলনা করা সহজ,

আমাদের যে কাজটা করতে হবে সেটা হল একটা ভ্যারিয়েবল বাছাই করে প্রত্যেকটা ভ্যারিয়েবলের সাথে কো রিলেশন বের করতে হবে (এমনকি তার নিজের সাথেও)। এটা করার জন্য আমরা ভ্যারিয়েবল গুলো Row এবং Column wise সাজাব,

----	num_preg	glucose_conc	diastolic_bp	thickness	insulin	bmi	age
num_preg	1	corr_value	corr_value	corr_value	corr_value	corr_value	corr_value
glucose_conc	corr_value	1	corr_value	corr_value	corr_value	corr_value	corr_value
diastolic_bp	corr_value	corr_value	1	corr_value	corr_value	corr_value	corr_value
thickness	corr_value	corr_value	corr_value	1	corr_value	corr_value	corr_value
insulin	corr_value	corr_value	corr_value	corr_value	1	corr_value	corr_value
bmi	corr_value	corr_value	corr_value	corr_value	corr_value	1	corr_value
age	corr_value	corr_value	corr_value	corr_value	corr_value	corr_value	1

আগেই বলা হয়েছিল, কোন ভ্যারিয়েবলের নিজের সাথে কো রিলেশন সবসময় 1 হবে। টেবিলের ডায়াগনাল বরাবর যত মান আছে সব অবশ্যই 1 হবে কারণ তাদের নিজেদের মধ্যে কো-রিলেশন বের করা হয়েছে। আর corr_value দ্বারা বুঝানো হয়েছে একটা ভ্যারিয়েবল ও আরেকটা ভ্যারিয়েবলের কো-রিলেশন কোন একটা ভ্যালু হতে পারে, যেহেতু আমরা লাইব্রেরি ব্যবহার করে এই ভ্যালুগুল‌ো নির্ধারণ করব তাই আমাদের নিজেদের হাতে ক্যালকুলেট করার প্রয়োজন দেখছি না।

এবার যেটা গুরুত্বপূর্ণ কাজ সেটা হল হিটম্যাপের রং বাছাই করা। চিন্তা করার কিছু নাই, Matplotlib লাইব্রেরির বিল্ট ইন কালার ম্যাপ দেখেই আমরা আপাতত কাজ করতে পারব। আপনি চাইলে ডকুমেন্টেশন ঘেঁটে নিজের পছন্দমত রং দিতে পারেন। আপাতত আমরা ডিফল্টটাই ব্যবহার করব।

Matplotlib Heat Map Color Guide

Matplotlib হিটম্যাপ জেনারেট করার সময় নিচের সিকোয়েন্স অনুযায়ী রং সেট করবে।

Less Correlated to More Correlated
Blue -> Cyan -> Yellow -> Red -> Dark Red (Correlation 1)

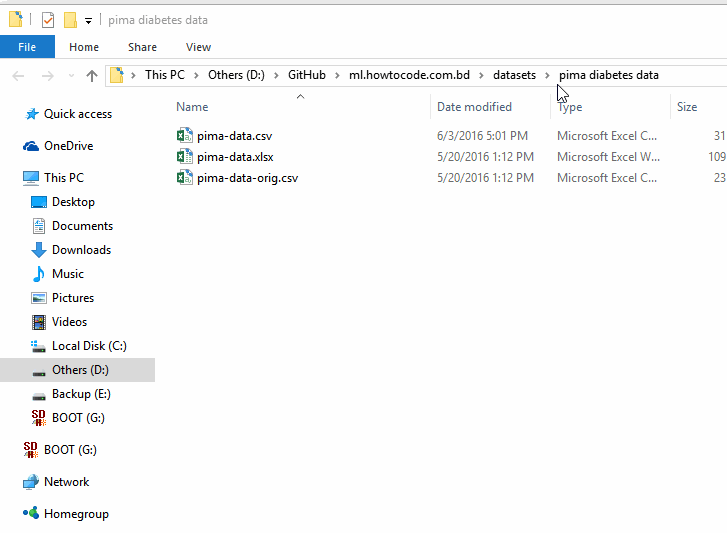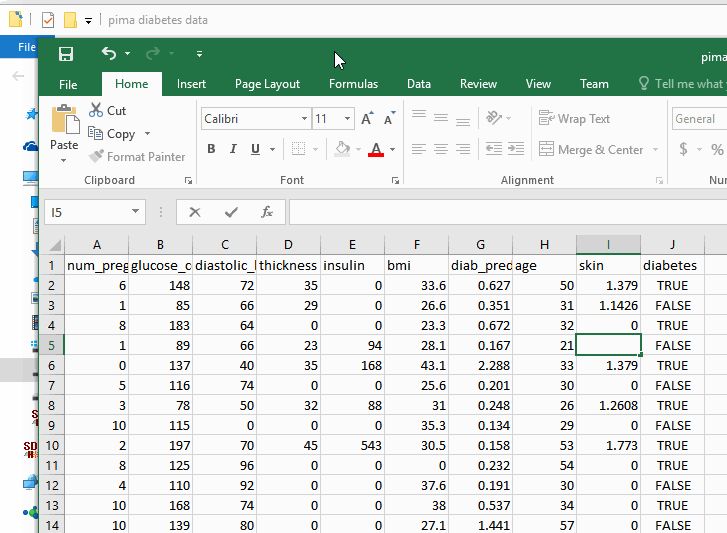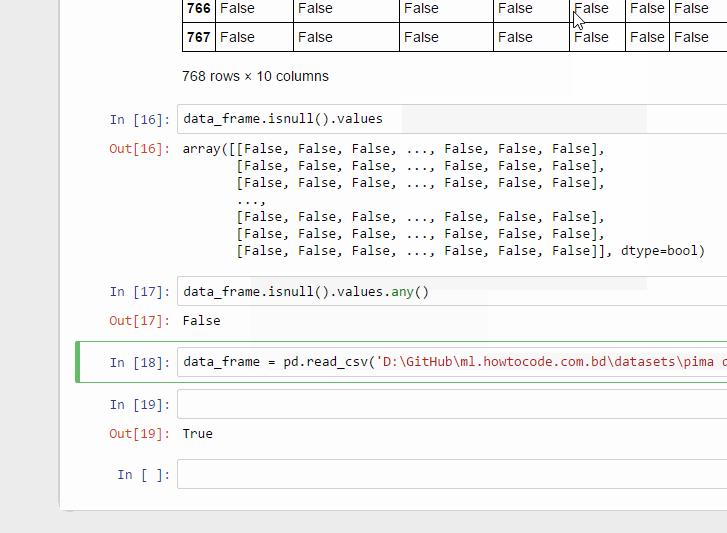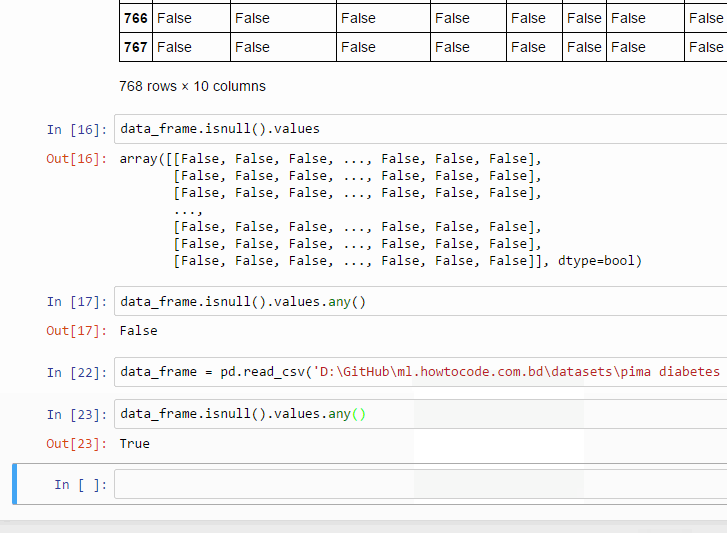
Heatmap জেনারেট করার ফাংশন

চলুন, চটপট হিটম্যাপ জেনারেট করার ফাংশন লিখে ফেলি, ফাংশনটা হবে এরকম

# Here size means plot-size
def corr_heatmap(data_frame, size=11):
  # Getting correlation using Pandas
  correlation = data_frame.corr()

  # Dividing the plot into subplots for increasing size of plots
  fig, heatmap = plt.subplots(figsize=(size, size))

  # Plotting the correlation heatmap
  heatmap.matshow(correlation)

  # Adding xticks and yticks
  plt.xticks(range(len(correlation.columns)), correlation.columns)
  plt.yticks(range(len(correlation.columns)), correlation.columns)

  # Displaying the graph
  plt.show()

কেন সাবপ্লট ব্যবহার করলাম?

ইচ্ছা করলে এখানে plt.matshow(correlation) ব্যবহার করেও হিটম্যাপ জেনারেট করা যেত, কিন্তু তাতে আমি ইচ্ছামত আকারের গ্রাফ জেনারেট করতে পারতাম না, তাই প্লটকে সাবপ্লটে নিয়ে সাইজ অ্যাসাইন করে ইচ্ছামত আকারের সুবিধাজনক প্লট জেনারেট করা যাচ্ছে।

xticks ও yticks কী?

plt.xticks(range(len(correlation.columns)), correlation.columns) এই কোড দিয়ে বুঝানো হয়েছে, প্রতি ব্লকের দৈর্ঘ্য হবে 1 একক করে এবং দাগগুলো হবে 0, 1, 2 ... len(correlation.columns) পর্যন্ত। আর পরবর্তী আর্গুমেন্ট (correlation.columns) দিয়ে প্রতিটা ব্লকের লেবেল দেওয়া হয়েছে।

plt.yticks.. এর জন্য একই কথা প্রযোজ্য।

plt.show() দিয়ে কী করা হয়েছে?

U kiddin' bro?

corr_heatmap(data_frame, size) ফাংশনের মাধ্যমে হিটম্যাপ প্লটিং

কষ্ট করে ফাংশন লিখলাম আর না ব্যবহার করলে চলে? নিচের কোড স্নিপেট দিয়ে সহজেই হিটম্যাপ প্লট করতে পারি,

corr_heatmap(data_frame)

heatmap

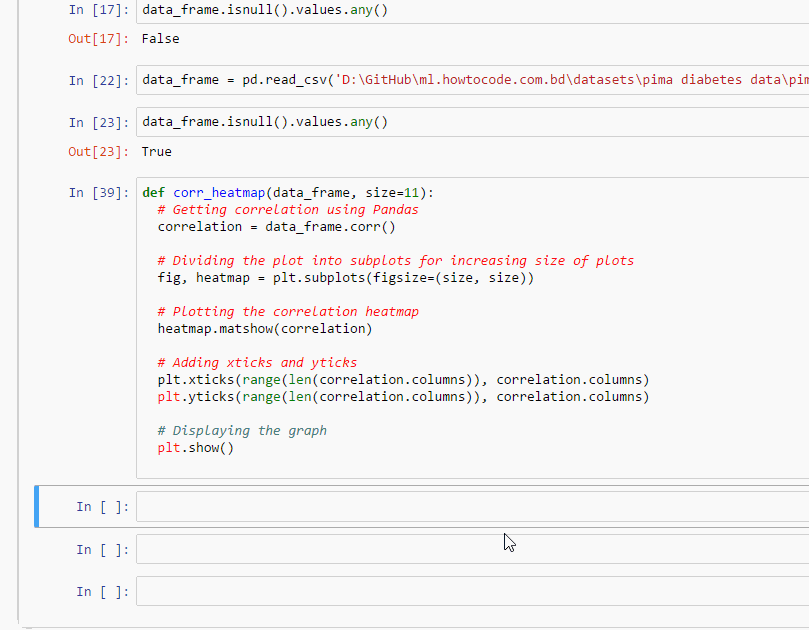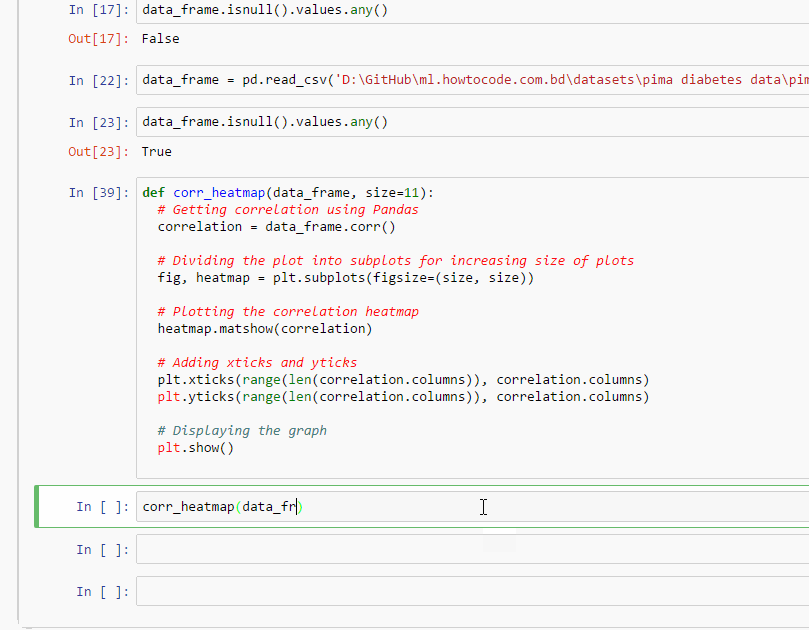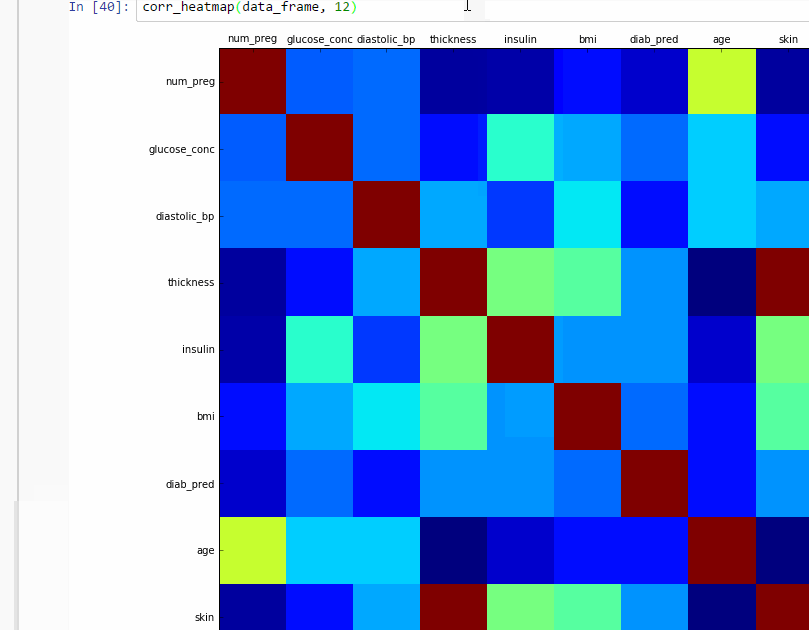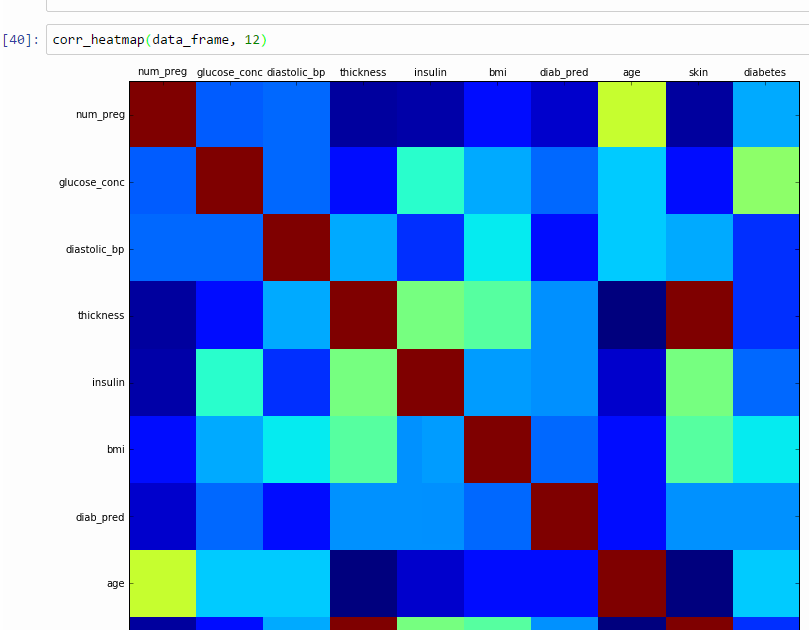
জেনারেটেড হিটম্যাপ ক্লোজভিউ

heatmapcloser

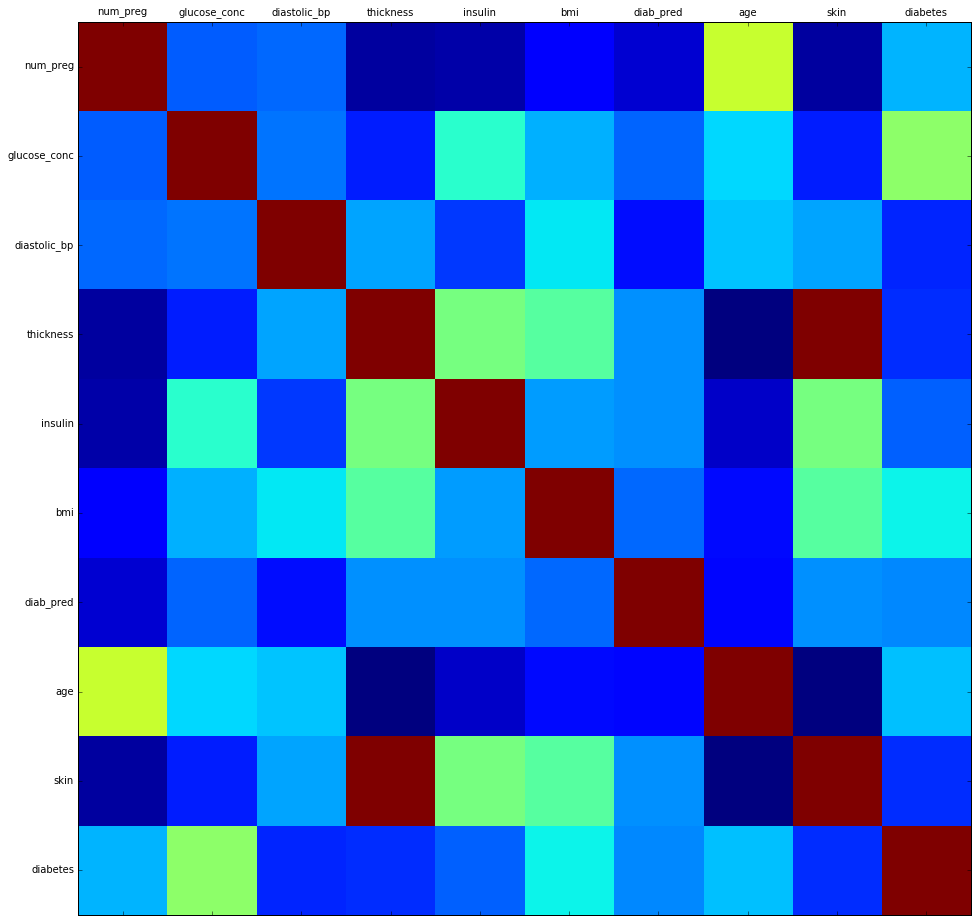
লক্ষণীয়

আমরা আগেই দেখেছিলাম দুইটা ভ্যারিয়েবল যদি একই রকম হয় তাহলে তাদের Correlation 1 হবে। ডায়াগনালে প্রতিটা ভ্যারিয়েবলে তার নিজের সাথে কো-রিলেশন বের করা হয়েছে তাই ডায়াগনালের ব্লকগুলোর রং গাঢ় লাল।

কিন্তু ভাল করে লক্ষ করে দেখবেন, skin এবং thickness এই দুইটার কো-রিলেশন কিন্তু 1 (গাঢ় লাল রং)।

তারমানে, skin আর thickness আসলে একই জিনিস, একক এর হেরফের হয়েছে শুধু। বিশ্বাস হচ্ছে না?

এক কাজ করুন তাহলে, thickness এর প্রতিটা ভ্যালু কে 0.0393701 দিয়ে গুণ দিন তাহলে দেখবেন আপনি skin এর ভ্যালু পেয়ে যাচ্ছেন। 1 millimeter = 0.0373701 inch এবার আপনিই বলতে পারবেন কোনটার একক আসলে কী?

কালপ্রিট পেলাম, এবার ডেটাসেট ক্লিনিং

উপরের কাজ থেকে এটা বুঝলাম আমরা যে একই টাইপের কলাম কোনগুলা। Tidy Data এর বৈশিষ্ট ছিল প্রতিটা কলাম কে অবশ্যই Unique হতে হবে। ডুপ্লিকেটগুলো থেকে একটা রেখে বাকিটা ডেটাসেট থেকে উধাও করতে হবে।

আমি এখানে skin ভ্যারিয়েবল উধাও করব, আপনি চাইলে একে অথবা thickness কে উধাও করতে পারেন, সম্পূর্ণ আপনার ইচ্ছা।

# Deleting 'skin' column completely
del data_frame['skin']
# Checking if the action was successful or not
data_frame.head()

vanish

আমরা একটা ডুপ্লিকেট কলাম কে ফেলে দিতে পারলাম। এখনো কাজ শেষ হয় নাই, ডেটা মোল্ড করতে হবে। চিন্তার কিছু নাই, ডেটা প্রিপারেশনের এটাই শেষ ধাপ। So cheers!

ডেটা মোল্ডিং (Data Molding)

ডেটা টাইপ অ্যাডজাস্টমেন্ট

আমাদের ডেটাসেট এমন হতে হবে তা যেন সবরকম অ্যালগরিদমে কাজ করার উপযোগী হয়। না হলে প্রতিটা অ্যালগরিদমের জন্য আমাদের ডেটা টুইকিং করতে হবে যেটা বেশ ঝামেলার কাজ। তাই আমরা ঝামেলার কাজটা বার বার না করে একবারই করব যাতে আর সেটা মাথাব্যাথার কারণ না হয়ে দাঁড়ায়।

ডেটা টাইপ চেকিং

ডেটা মোল্ডিংয়ের আগে একবার ডেটাটাইপ গুলো চেক করে নেওয়া যাক।

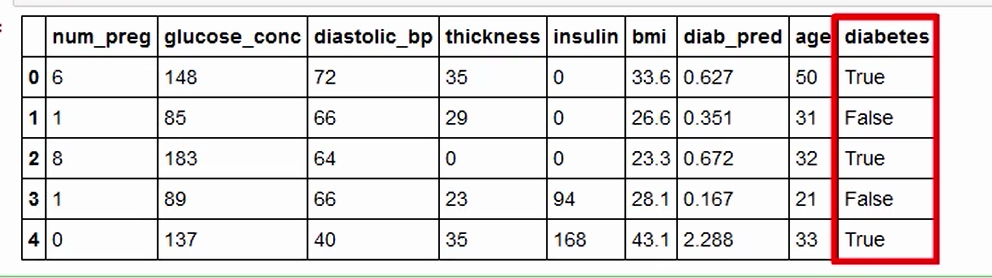
data_frame.head()

এটা দিলেই আবারও ডেটাফ্রেমের কিছু স্যাম্পল দেখতে পাবেন এবং ভাল করে লক্ষ করে দেখবেন এখানে সবগুলো ভ্যালুই ফ্লোট বা ইন্টিজার টাইপ কিন্তু একটা রয়ে গেছে Boolean টাইপ।

type

ডেটা টাইপ চেঞ্জিং

True কে আমরা 1 বানাবো এবং False কে বানাব 0। নিচের কোড স্নিপেট টি দিয়েই কাজটা করা যাবে,

# Mapping the values
map_diabetes = {True : 1, False : 0}

# Setting the map to the data_frame
data_frame['diabetes'] = data_frame['diabetes'].map(map_diabetes)

# Let's see what we have done
data_frame.head()

typechange

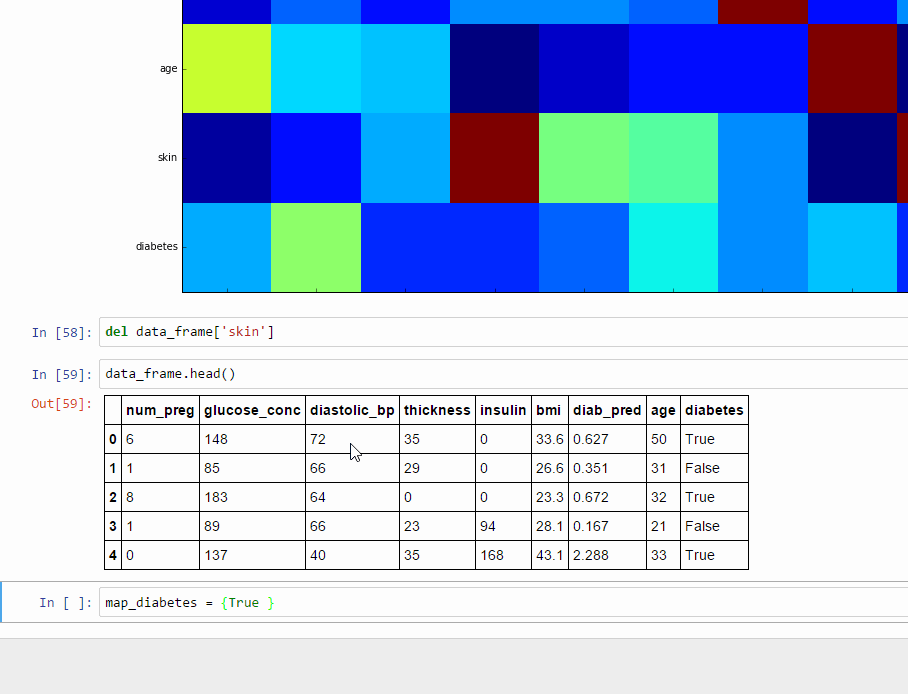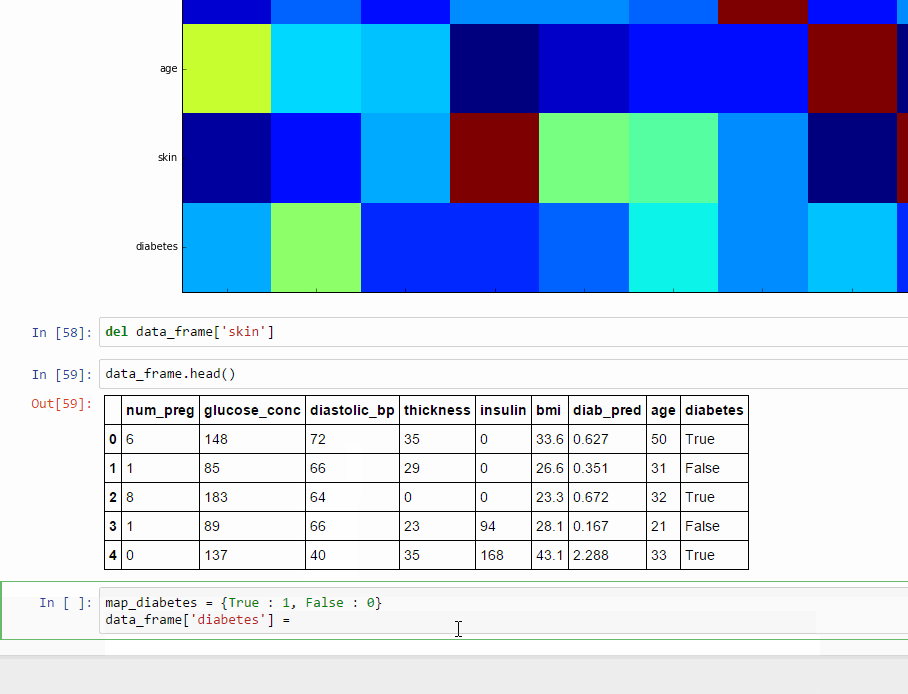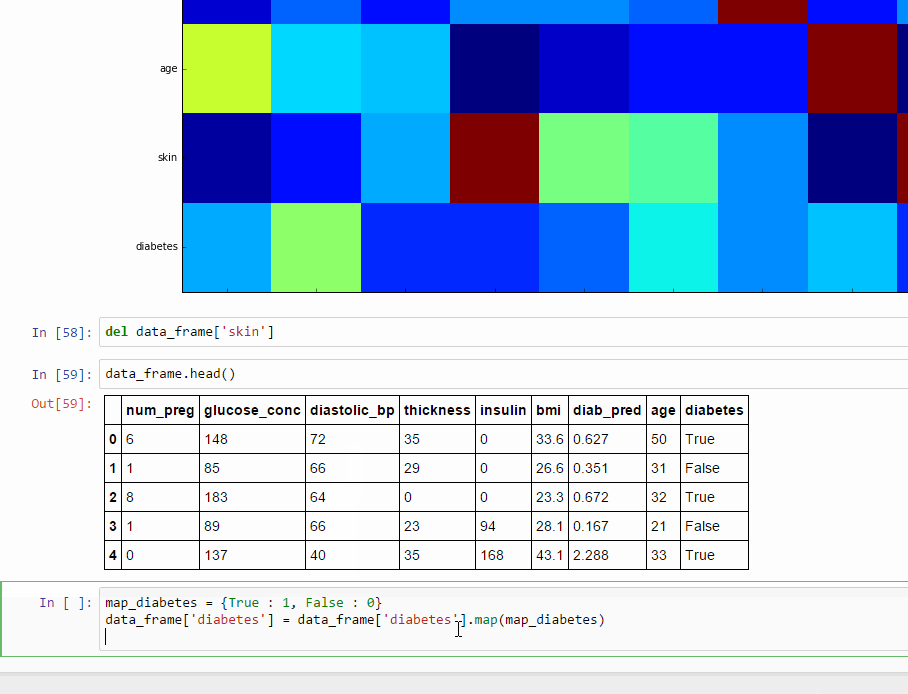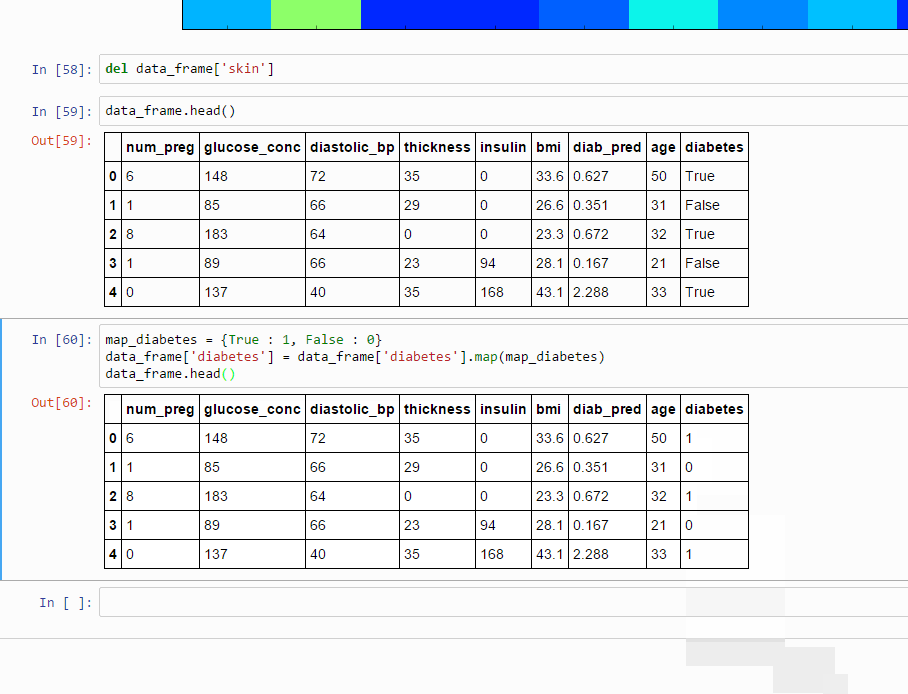
অভিনন্দন!

এই মোল্ডেড ও ক্লিনড ডেটাসেট আমরা আমাদের ইচ্ছানুযায়ী অ্যালগরিদমে বসিয়ে কাজ করতে পারবো।

কিন্তু?

Data Rule #3

Rare ইভেন্ট হাই অ্যাকুরেসির সাথে প্রেডিক্ট করার সম্ভাবনা কম

স্বাভাবিক, কারণ Rare ইভেন্ট মানে আপনার ডেটাসেট এ এইরকম ইভেন্ট কম থাকবে। আর এইরকম ইভেন্টের ডেটাসেট যত কম থাকবে প্রেডিকশন ও ততটাই খারাপ আসবে। তবে এটা নিয়ে চিন্তা না করাই ভাল। আগে গতানুগতিক প্রেডিকশন ঠিক করেন, পরে না হয় রেয়ার ইভেন্ট ঠিক করলেন।

আরও কিছু অ্যানালাইসিস।

True / False Ratio চেক করা

আমরা চাইলে দেখতে পারি, এই ডেটাসেট এ শতকরা কতজন ডায়বেটিসে আক্রান্ত আর কতজন নয়, নোটবুক বের করে ঝটপট কোড লিখে ফেলেন।

num_true = 0.0
num_false = 0.0
for item in data_frame['diabetes']:
    if item == True:
        num_true += 1
    else:
        num_false += 1

percent_true = (num_true / (num_true + num_false)) * 100
percent_false = (num_false / (num_true + num_false)) * 100

print ("Number of True Cases: {0} ({1:2.2f}%)".format(num_true, percent_true))
print ("Number of False Cases: {0} ({1:2.2f}%)".format(num_false, percent_false))

আউটপুট:

Number of True Cases: 268.0 (34.90%)
Number of False Cases: 500.0 (65.10%)

আমরা Pythonic Way তে কোডটা আসলে চার লাইনে লিখতে পারি।

# Pythonic Way
num_true = len(data_frame.loc[data_frame['diabetes'] == True])
num_false = len(data_frame.loc[data_frame['diabetes'] == False])
print ("Number of True Cases: {0} ({1:2.2f}%)".format(num_true, (num_true / (num_true + num_false)) * 100))
print ("Number of False Cases: {0} ({1:2.2f}%)".format(num_false, (num_true / (num_true + num_false)) * 100))

‍‍‍

Data Rule #4

ডেটা ম্যানিপুলেশন হিস্ট্রি রাখবেন ও চেক করবেন নিয়মিত

• এটা করার জন্য একটা ব্যবস্থা আছেই (Jupyter Notebook ব্যবহার করে)

• ভার্সন কন্ট্রোল সিস্টেম ব্যবহার করে, যেমন : Git, SVN, BitBucket, GitHub, GitLab ইত্যাদি

সামারি

কী কী করলাম এই দুই পর্বে?

• Pandas দিয়ে ডেটা রিড করলাম

• কো-রিলেশন সম্পর্কে ধারণা নিলাম

• ডুপ্লিকেট কলাম উচ্ছেদ করলাম

• ডেটা মোল্ড করলাম

• True/False রেশিও চেক করলাম

So far so good, পরবর্তী পর্বে আশা করি আমরা অ্যালগরিদম অ্যাপ্লাই করে প্রেডিক্ট করা শুরু করে দিব।