মডেল পারফর্মেন্স টেস্টিং - শেষ পর্ব
মডেল পারফর্মেন্স - দ্বিতীয় এবং শেষ পর্ব
আমরা মেশিন লার্নিংয়ের একদম শেষ পর্বে চলে এলাম। আগের পর্বেই মোটামুটি দেখেছিলাম মডেল ভাল পারফর্ম না করলে অথবা অন্য মডেল আদৌ ভাল পারফর্ম করছে কিনা সেটা জানার জন্য কীভাবে কাজ আগাতে হয়।
যেসব টপিক আলোচনা করা হয়েছে (টিক দেওয়া) এবং যেসব টপিক নিয়ে আলোচনা করা হয় নাই (টিক ছাড়া)
আমরা এখনো এই ধাপে,

মডেল পারফর্মেন্স রিভিশন - ROC
ROC বোঝার আগে অবশ্যই Confusion Matrix সম্পর্কে জানতে হবে, না জানলে আগের পর্ব থেকে পড়ে নিন।
ROC স্পেসে ROC কার্ভ আঁকার জন্য X-axis এ FPR (False Positive Rate) ও Y-axis এ TPR (True Positive Rate) বসাতে হয়।
তারমানে কনফিউশন ম্যাট্রিক্স থেকে প্রাপ্ত TPR ও FPR রেট বসালে আমরা একটা পয়েন্ট পাব, এভাবে একই ডেটাসেটের উপর প্রয়োগকৃত যতগুলা মডেল নিয়ে আমরা কাজ করব সেগুলোর প্রতিটি থেকে একটি করে পয়েন্ট পাব।
এই পয়েন্টগুলো যোগ করে দিয়ে গ্রাফ আঁকলেই আপনি পেয়ে যাবেন আপনার আকাঙ্ক্ষিত ROC কার্ভ।
একটা পার্ফেক্ট ক্লাসিফায়ারের TPR হয় 1 এবং FPR হয় 0।
একটি উদাহরণ দিয়েই ROC বোঝা যায়।
একটা সিনারিও দেখা যাক,
আমি একটা ডায়বেটিস ডেটাসেট নিলাম, ডেটাসেট এ Observation আছে 1000 টা, আমি এটাকে 80%-20% এ ভাগ করলাম। তারমানে 80% ডেটা হল ট্রেইনিং ডেটা, 20% ডেটা হল টেস্টিং ডেটা।
আবার ধরুন, 200 টা টেস্টিং ডেটার মধ্যে 100 টা হল Positive (মানে আউটপুট পজিটিভ আরও সহজভাবে বললে ঔ ১০০ টা ডেটার আউটকাম হল ডায়বেটিস হয়েছে)। এবং 100 টা Negative।
আমি চারটা মডেল তৈরি করলাম, এই মডেল চারটা আমি ট্রেইন করব ও তাদের পারফর্মেন্স টেস্ট করব। চারটা মডেল হল,
Gaussian Naive Bayes Model
Logistic Regression Model
Random Forest Model
Artificial Neural Network Model
আমরা এখনো Artificial Neural Network দেখি নাই এবং এটা সম্পর্কে না জানলেও সমস্যা নেই।
আমি আগের পর্বের মত করে প্রতিটা মডেলকে ট্রেইন করে তারপর তাদের Confusion Matrix বের করতে পারি, তাই না? ঠিক সেভাবেই আমি 80% ডেটাসেট দিয়ে মডেলগুলোকে শিখিয়ে পড়িয়ে মানুষ করব তারপর তাদের পারফর্মেন্স টেস্ট করার জন্য পড়া ধরব। (কনফিউশন ম্যাট্রিক্স বের করব)।
আরও মনে করতে থাকেন, প্রতিটি মডেলের Confusion Matrix ও পাশাপাশি তাদের TPR, FPR বের করলাম।
Gaussian Naive Bayes Model
TP = 63
FP = 28
FN = 37
TN = 72
Logistic Regression Model
TP = 77
FP = 77
FN = 23
TN = 23
Random Forest Model
TP = 24
FP = 88
FN = 76
TN = 12
Artificial Neural Network Model
TP = 76
FP = 12
FN = 24
TN = 88
আমরা আগেই জেনেছি ROC Curve এর ক্ষেত্রে Y-axis এ থাকে TPR এবং X-axis এ থাকে FPR। তাহলে আমরা এই চারটা Coordinate সহজেই ROC Space এ বসাতে পারি।
Coordinate গুলো
এই পয়েন্টগুলো আমরা এখন প্লট করব।
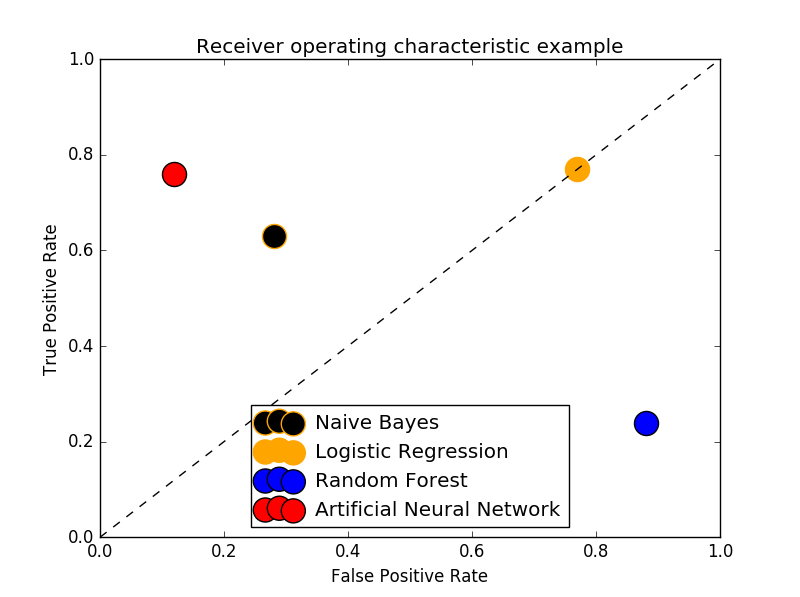
উদাহরণটি উইকিপিডিয়া থেকে নেয়া, উইকিপিডিয়ার ROC কার্ভে অতিরিক্ত কিছু জিনিস পয়েন্ট আউট করে দেওয়া আছে,

আমি এখানে প্রতিটি পয়েন্ট বোঝানোর জন্য আলাদা ভাবে স্ক্যাটার প্লট করেছি। আপনার যদি মডেল অনেকগুলো হয় কিংবা, একই মডেলের প্যারামিটার পরিবর্তনভিত্তিক পারফর্মেন্স যদি আপনি প্লট করেন তাহলে আপনার প্লট করা ROC কার্ভ হবে এইরকম।

আমার এখানে মডেল মাত্র ৪ টা, তাই এখানে লাইন প্লট করলে বোঝা যাবে না তাই, স্ক্যাটার প্লট করা হল।
ROC Curve ব্যাখ্যা
100% Accurate Model এর FPR = 0 এবং TPR = 1। এটাকে আইডিয়াল ধরে সহজেই বোঝা যাচ্ছে ANN মডেল হিসেবে সবেচেয়ে ভাল, তারপর Naive Bayes, তারপর Logistic Regression এবং সবার শেষে Random Forest পারফর্ম করেছে।
আগেই (এবং আবারো) বলে রাখি, সবসময় ANN > NB > LR > RF এইরকম হবে তা নয়, ডেটাসেট ও প্রবলেমের ধরণ অনুযায়ী এক এক মডেলের পারফর্মেন্স একেক রকম। আমি এখানে পুরো ব্যাপারটা কল্পনা করেছি।
মাঝখান দিয়ে যে ড্যাশড লাইন কোণাকুণি বরাবর গিয়েছে তাকে বলে Line of no-discrimination। পয়েন্ট যত এই লাইনের উপরে থাকবে তত ভাল এবং নিচে থাকলে ততটাই খারাপ।
AUC বা Area Under Curve
উপরে একটা ROC Curve দেখছেন নিশ্চয়? সেখানে ROC কার্ভ যতটা Area কভার করে ততটাই ভাল। 100% Accurate Model এর AUC হল TPR * FPR বা পুরো গ্রাফের ক্ষেত্রফল।
AUC দিয়ে পারফর্মেন্স পরিমাপ করা নিয়ে অনেক প্রশ্ন উঠেছে বর্তমানে, সবাই কমবেশি ROC প্রেফার করে । তাই AUC নিয়ে কথা বাড়ালাম না।
ওভারফিটিং
আগেও বলা হয়েছিল, কোন কোন সময় মডেলের পারফর্মেন্স এতটাই ভাল হয় যে Training Data এর ক্ষেত্রে Accuracy Rate প্রায় 95-99% হয়। কিন্তু Testing Data তে প্রেডিক্ট করতে দিলে 40% Accuracy Rate ও হয় না।
প্রশ্ন হচ্ছে, এটা কেন হয়?
আসলে আমরা যে ডেটাসেট দিয়ে ট্রেইন করি, সেখানে আসল ডেটার পাশাপাশি Noise ও থাকে। অর্থাৎ, 100% Pure Dataset আপনি কখনোই পাবেন না।
একটা ক্লাসিক এক্সাম্পল হতে পারে, আমি কিছু ডেটাসেট জোগাড় করলাম, কয় ঘণ্টা পড়ি আর কয় ঘণ্টা ঘুমাই তার উপর কত মার্কস পাই। এখন আমি এই ডেটাসেট এর উপরে মডেল ট্রেইন করে প্রেডিক্ট করতে বসে যাই এবং যদি কোনভাবে দেখি, পড়া কমিয়ে ঘুমালে মার্কস বেশি আসছে, এবং সেটার উপর ভিত্তি করে আমি পরবর্তী পরীক্ষার আগে ঘুমায়ে কাটালাম কিন্তু পড়লাম না একটুও (কারণ আমার তৈরি A.I বলেছে ঘুমালে মার্কস বেশি পাওয়া যাবে)। তাতে ফলাফল কী আসবে সেটা বোঝাই যাচ্ছে।
তাহলে এই যে ভুলভাল প্রেডিকশন দিচ্ছে, তার কারণ কী? দুইটা কারণ, (১) পর্যাপ্ত পরিমাণ ডেটা নাই, (২) ডেটাসেট এ কলামের সংখ্যা (ভ্যারিয়েবল, এখানে যেমন কয় ঘণ্টা পড়ি আর কয় ঘণ্টা ঘুমাই) কম। মার্কস ভাল আসার অনেক কারণ থাকতে পারে, পরীক্ষা যদি MCQ হয় আর তাতে ঝড়ে বক দিয়ে ভাল পরিমাণ দাগিয়ে ফেললাম, অথবা প্রশ্ন অনেক সহজ হল ইত্যাদি। তাহলে এগুলোতো আমি ইনপুট এ না দিয়েই ট্রেইন করেছি, তাই মডেল স্বভাবতই সেই ? কারণ গুলো না জেনেই আমার দেওয়া ডেটাসেট এর সাথে নিজেকে এমন ভাবে খাপ খাওয়াবে তাতে Error সবচেয়ে কম থাকে।
মডেল ট্রেইন মানে হচ্ছে Error কমানো, আর Error কমানোর জন্য প্রতিটি মডেলের হাইপারপ্যারামিটার গুলো ম্যাথেমেটিক্যাল অ্যানালাইসিস অনুযায়ী সেট হয়। যে হাইপারপ্যারামিটার ব্যবহার করলে Error সবচেয়ে কম হবে সেটাই মডেল ব্যবহার করবে (এটাই স্বাভাবিক)। কিন্তু Error কম করতে গিয়ে যদি Model, ডেটাসেটের Noise এর সাথে খাপ খাইয়ে নেয় তাহলে যথেষ্ট ঝামেলা হবে।
ওভারফিটিং সম্পর্কে পরবর্তীতে আমরা আরও বিস্তারিত দেখব কয়েকটি ধাপে।
ওভারফিটিং কমানো
ওভারফিটিং কমানোর জন্য যেটা করা যায় সেটা হচ্ছে, ডেটা জোগাড় করা এবং কলামের সংখ্যা বাড়ানো। যতটা পিওর সম্ভব ততটা পিওর ডেটাসেট ও ভাল প্রেডিকশন রেজাল্ট দিতে পারে। এটাতো গেল ডেটাসেট এ কি করবেন। চাইলে অ্যালগরিদম টিউন করেও ভাল রেজাল্ট বের করা সম্ভব। আমরা একটা মেথড দেখব।
Regularization & Regularization Hyperparameter
একটা অ্যালগরিদম কীভাবে শিখবে সেটা আমরা চাইলে কন্ট্রোল করতে পারি। মেশিন লার্নিং অ্যালগরিদম মানেই তার পিছনে কোন না কোন ম্যাথমেটিক্যাল মডেল কাজ করছে, তাই সেই ম্যাথমেটিক্যাল মডেলের লার্নিং মেকানিজম চাইলে কিছু নির্দিষ্ট প্যারামিটার দিয়ে কন্ট্রোল করা যায়।
ধরি কোন একটি মডেল আউটপুট বের করে এই সূত্র দিয়ে,
Y=ax3+bx
আমরা এর লার্নিং কন্ট্রোল করার জন্য, (x×λ) অংশ রেজাল্ট থেকে বিয়োগ দিয়ে Regularized Model তৈরি করতে পারি,
Y=ax3+bx−λ×x
এখানে,λ ই হল Regularization Hyperparameter।
লক্ষণীয়, Y এর মান আগের প্রেডিকশনের থেকে কিছুটা কম আসবে, তারমানে আমি এবার Training Dataset এই Accuracy আগের চেয়ে কম পাব। কিন্তু এটা ভাল! কারণ? কারণ হচ্ছে , এবার সে প্রতিটা ডেটাসেট মুখস্ত করছে না, কারণ Regularization Hyperparameter তাকে মুখস্ত করতে দিবে না, x এর মান যত বাড়বে, তার প্রেডিক্টেড ভ্যালু ততটাই পেনাল্টি খাবে। একে আমরা তাই Penalized Machine Learning Model বলতে পারি।
যখনই মডেলটা এরর কমানোর জন্য ডেটাসেট এর সাথে খাপ খাওয়াতে যাবে, ওমনি lambda তাকে পেনাল্টি দিয়ে দূরে সরিয়ে দেবে। আমাদের আল্টিমেট কাজ হবে এই lambda কে এমন ভাবে টিউন করা যাতে Testing Dataset এ অ্যাকুরেসি ভাল আসে। Training Dataset এ অ্যাকুরেসি গোল্লায় যাক :P
Logistic Regression মডেলে Regularization Hyperparameter টিউনিংয়ের মাধ্যমে অ্যাকুরেসি বাড়ানো
টপিকের টাইটেল একটু বড় হয়ে গেল। একটু আগে আমরা জানলাম, ম্যাথমেটিক্যাল মডেল হ্যাক করে আমরা Regularization এর মাধ্যমে মডেলের ওভারফিটিং কমাতে পারি। মডেল ভিত্তিক Regularization Hyperparameter বিভিন্ন হয়। সাইকিট লাইব্রেরিতে অলরেডি Logistic Regression এর মডেলের কোড করে দেওয়া আছে এবং তারা Regularization Hyperparameter চেঞ্জ করার জন্য সুবিধাজনক ইন্টারফেসও দিয়েছে।
আমাদের কাজ হবে, Regularization Hyperparameter এর মান পরিবর্তন করে প্রেডিকশন স্কোর সংগ্রহ করা। তারপর যে Hyperparameter Value তে প্রেডিকশনের অ্যাকুরেসি সর্বোচ্চ হবে সেটা স্টোর করে রাখা।
থিওরি দেখলাম, এবার প্র্যাক্টিক্যাল দেখার পালা। এখন আপনাকে অবশ্যই নোটবুক বের করে কোড লিখতে হবে।
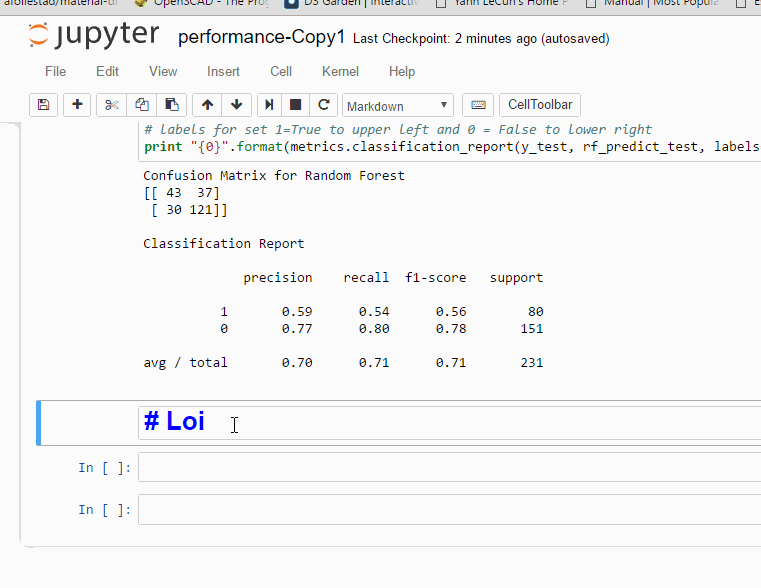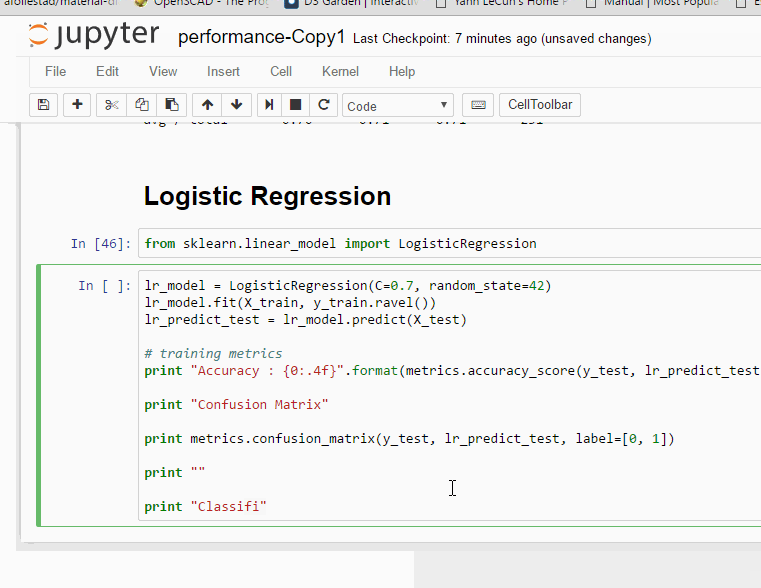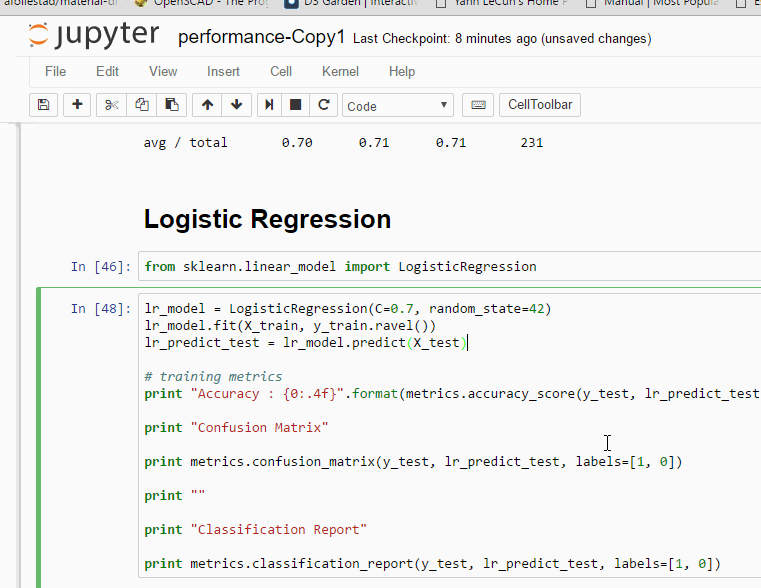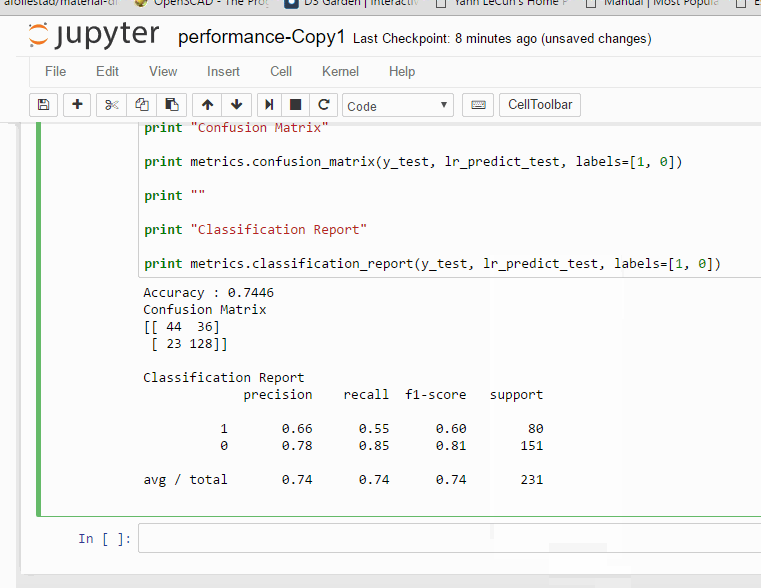
আউটপুট
এই কাজগুলো আমরা নাইভ বেয়েস মডেলের জন্য করেছিলাম। এখানে C হচ্ছে আমাদের সেই Regularization Hyperparameter, শুরুতে ধরে নিলাম 0.7, আমরা পরে এর বিভিন্ন মানের জন্য অ্যাকুরেসি চেক করব।
C (Regularization Hyperparameter) এর মান নির্ণয়
যেহেতু Regularization Hyperparameter C, আর আমি বিভিন্ন C এর মানের জন্য recall_scores দেখতে চাচ্ছি (recall_score যত বেশি তত ভাল), তাই C_start = 0.1 নিলাম, C_end = 5 নিলাম, আর লুপে C এর মান 0.1 করে বৃদ্ধি করলাম।
আর প্রতি C এর ভ্যালুর জন্য প্রেডিক্টেড ডেটাসেট দিয়ে অ্যাকুরেসি চেক করলাম, যখনই recall এর মান আগেরটার চেয়ে বেশি হবে তখনই best_recall_score এ recall_score অর্থাৎ বর্তমান স্কোর অ্যাসাইন হবে।
আগের বিষয়গুলো বুঝতে পারলে কোডটা কঠিন কিছু নয়।
C_values এবং recall_scores নামের দুইটা লিস্ট রাখলাম ভ্যালু স্টোরের জন্য
আউটপুট
C এর মান বৃদ্ধির সাথে কীভাবে পারফর্মেন্স পরিবর্তন হচ্ছে তার গ্রাফ।
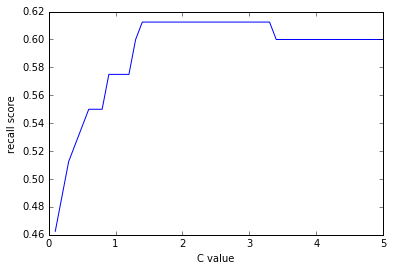
C এর মান যখন 2-3 এর মধ্যে তখন Recall Score সবচেয়ে বেশি, C এর মান 4-5 এবং 0-1 এর মধ্যে কম।
class_weight = 'balanced' ও C পরিবর্তনের সাথে মডেল পারফর্মেন্স
class_weight = 'balanced' ও C পরিবর্তনের সাথে মডেল পারফর্মেন্সRegularization Hyperparameter একটাই হবে তার কোন কারণ নেই, একাধিক থাকতে পারে। একটু আগে আমরা C এর মান বের করেছিলাম। এখন আমরা আরেকটি প্যারামিটার (class_weight) কে balanced দিয়ে দেখব পারফর্মেন্স কিরকম দিচ্ছে।
class_weight = 'balanced' রেখে C এর মান পরিবর্তন করে পারফর্মেন্স বের করাই হবে মূল উদ্দেশ্য।
আউটপুট:
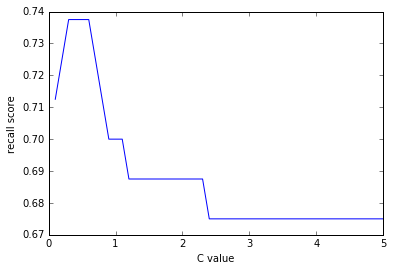
ক্লাস ওয়েট balanced দেওয়াতে দেখা যাচ্ছে Recall Score বেড়ে 0.73+ হয়েছে, definitely what we were looking for!
কনফিউশন ম্যাট্রিক্স
কোড:
আউটপুট:
Regularization এর মাধ্যমে এভাবে আমরা অ্যাকুরেসি বাড়াতে পারি (ওভারফিটিং কমিয়ে)।
K-Fold / N-Fold Cross-validation
ওভারফিটিং কমানোর আরেকটি ইফেক্টিভ অ্যালগরিদম হল K-Fold Cross-validation। নামটা অনেক কঠিন শোনালেও কাজ খুবই সহজ।
আমাদের ডায়বেটিস ডেটাসেট এ কিন্তু নেগেটিভ উত্তর বেশি (মানে ডায়বেটিস হয় নাই)। যেখানে ডেটাসেট এর ব্যালেন্স কম থাকবে সেসব ক্ষেত্রে K-Fold Cross-validation খুবই ভাল অ্যাকুরেসি দিতে সাহায্য করে।
K-Fold বা N-Fold Cross-validation একই জিনিস যখন k=N! বা K = Number of observation।
k-Fold Cross-validation এ যেটা করা হয়, সম্পূর্ণ ডেটাসেটকে k equal sized এ সাবস্যাম্পল করা হয়।
এবার এই k সংখ্যক সাবস্যাম্পল থেকে একটা একটা করে ডেটা নেয়া হয় টেস্টিং এর জন্য।
যেমন, আমার কাছে 25 টা অবসার্ভেশনের ডেটাসেট আছে, আমি এদেরকে ৫ টা গ্রুপে ভাগ করলাম।
তারমানে প্রতিগ্রুপে ডেটাসেট থাকল ৫ টা করে। এবার এই পাঁচটা গ্রুপের প্রথম গ্রুপ আমি Hold করলাম বাকিগুলো ট্রেইনিংয়ে দিলাম, Hold করা ডেটাসেট দিয়ে টেস্ট করলাম।
দ্বিতীয় Pass এ দ্বিতীয় গ্রুপ Hold করব (ট্রেনিংয়ে পাঠাব না), আর বাকিগুলো Training এ পাঠাব।
ঠিক একই ভাবে চতুর্থ এবং পঞ্চম Pass এ ঔ পজিশনাল গ্রুপটি Hold করে বাকিটা পাঠাব ট্রেইনিংয়ে।
এভাবে 5 বার 5-Fold এ ট্রেইন করব। যেহেতু প্রতি গ্রুপে Observation 5 টা এবং গ্রুপ সংখ্যা ৫ টা তাই এর নাম হবে 5-Fold Cross-validation।
Cross-validation ব্যবহার করে মডেল ট্রেইনিং ও টেস্টিং
ক্রস ভ্যালিডেশন এনাবলড মডেল সাইকিটে বানানোই আছে, যেকোন নরমাল মডেল এর সাথে CV লাগিয়ে দিলেই Cross-validation Enabled Model পেয়ে যাবেন।
যেমন, LogisticRegression এর Cross-validation Enabled মডেল হবে LogisticRegressionCV, এভাবে বাকিগুলোর জন্যও সত্য।
চলুন এটার পারফর্মেন্স দেখা যাক,
আউটপুট:
10-Fold ক্রস ভ্যালিডেশনে পারফর্মেন্স খারাপ আসে নি!
অনেক বড় হয়ে গেল চ্যাপ্টারটা, তবুও Bias-Variance টা বাদ থেকে গেল। পরবর্তী অন্য কোন পর্বে আমরা দেখব Bias-Variance Trade-off কী জিনিস এবং এর ইম্প্যাক্ট কতখানি।
Scikit-learn Algorithm Cheat Sheet
ডেটাসেট থেকে অ্যালগো সিলেকশনের উপরে সাইকিটের নিজস্ব একটা চিটশিট আছে। খুবই ইফেক্টিভ,
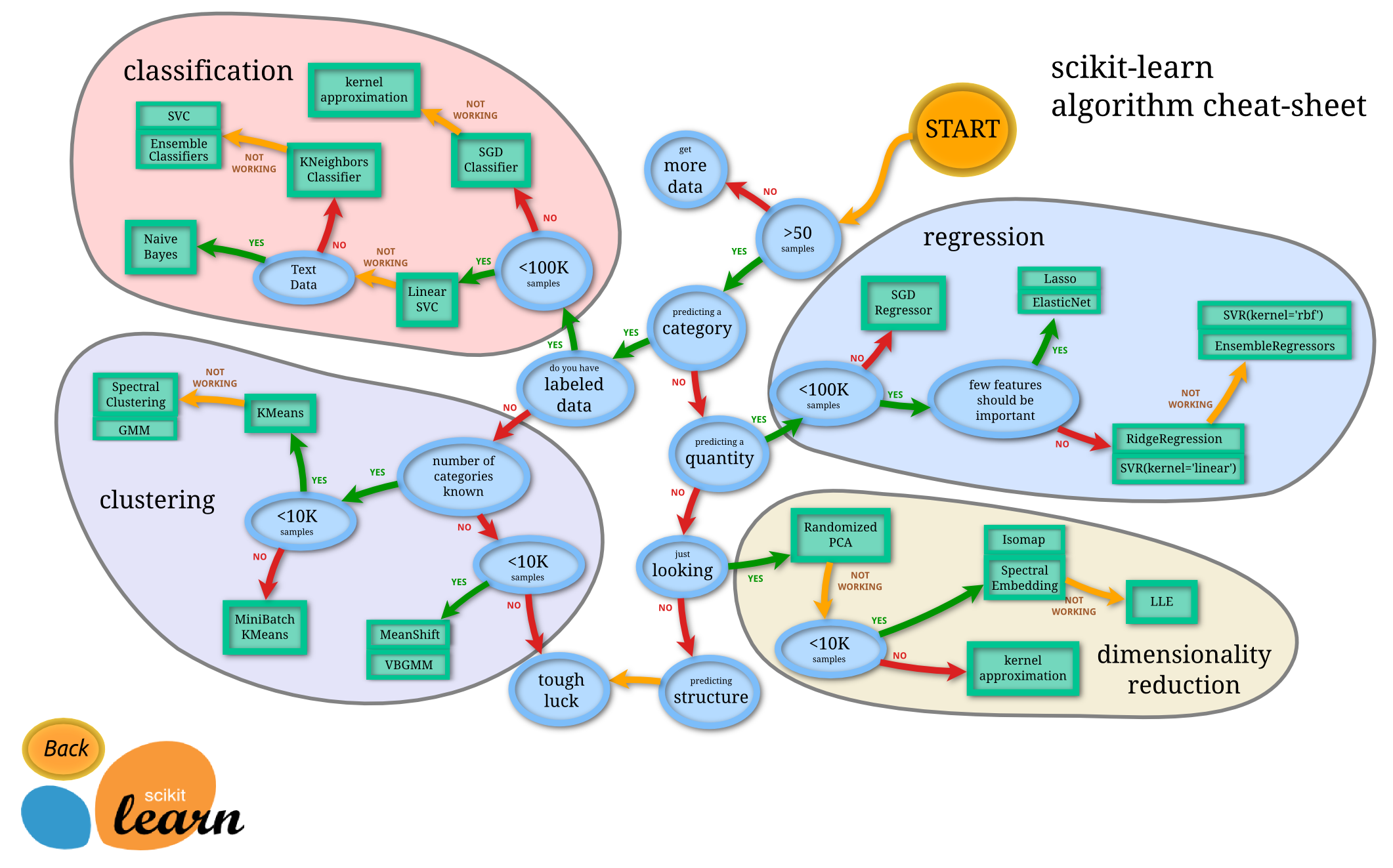
শেষ পর্যন্ত যেসব টপিক নিয়ে আলোচনা করা হল
Last updated